BT. A Runcinated Dodecaplex
We visit a giant model of a four-dimensional polyhedron, made of the fabulous Zome math construction toy. Paul Hildebrandt, president of Zome, weighs in!

This model is a three-dimensional shadow of a four-dimensional polyhedron. Though it looks quite complicated, it is merely divided into lots and lots of cells that are pretty simple: tetrahedra (blue in the fig below), dodecahedra (brown), and prisms (yellow and green).

Towards the boundary of the ball, the cells are increasingly foreshortened; this is exactly analogous to the way a two-dimensional picture of a three-dimensional polyhedron is a division of a disk into polygons that are increasingly foreshortened towards the edge of the picture.
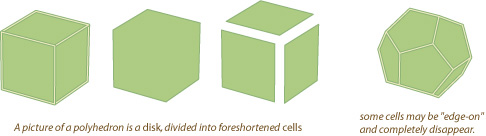
Just as the archimedean polyhedra are formed of polygons, the archimedean polytopes are formed of archimedean and regular polyhedra:
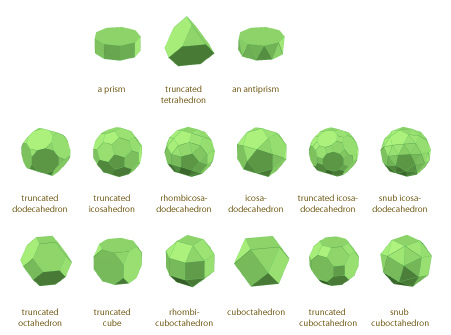
At some point we hope to get around to explaining this better.
In the meantime, we enthusiastically recommend
Here are some sites for intermediate to advanced adventurers; if someone knows of a beginner’s guide to the fourth dimension or has another link to recommend, please let us know!

 mathbun.com
mathbun.com