Strange appearance in the North Atlantic:

There has been a theme in some of the recent posts and problems. It’s a little buried but almost enough to say its another of those Mathfactor agendas when we try to sneak some knowledge to you buried in the fun.  Never one to miss such an opportunity I will jump in with a post, and a problem.  This is a slight change to a classic problem that comes out of the work of one of my mathematical heroes:  Leonardo of Pisa, also known as Fibonacci.  He is responsible for changing how we count! Not many people can claim that. He introduced the system base value, also known as Arabic numerals that we still use today into Europe.  He is more famous however for talking about rabbits:

Imagine that you have immortal rabbits, Bugs Bunny’s version of Olympus perhaps.  Even if they are immortal however rabbits are famous for one thing.  They breed like, well rabbits.  Some of the rabbits are children and some adults and are divided into pairs.  Each month any child pairs become adults and any adult pairs breed to produce a new child pair.  They are immortal so no pair ever dies.  These rabbits are also a little odd.  They live on a line (don’t complain, this is no more ludicrous than that they are immortal!), but can shuffle along.  Also if you are worried about inbreeding, the male rabbit leave the family hutch and shuffle along the line past others until they find a suitably unrelated mate.  Why we would be worried about inbreeding in immortal rabbits living on a line escapes me!

Anyway we start with one pair of children.  Lets put a c.  After a month they become adults, a.  Another month passes and they now have a pair of children, but are still there themselves.  We therfore have the original pair and a pair of children: ac.  Next month the adults have another pair of children and the children become adults: aca.  Can you see how this will work?  Each month the children become adults so we replace every c with and a, each pair of adults has a new pair of children but stays as adults, so we replace every a with ac.  We can continue to get longer and longer sequences of rabbits on this line:

aca  to acaac to acaacaca to acaacacaacaac….

Now some puzzles.  Given a line with 21 adult pairs and 13 child pairs, how many pairs of adults and children would there be after one month?

Given p adults and q children how many adults and children will there be after one month?

Finally a more difficult one.  How will the ratio of adults to children behave month on month?  Will it

a) Get closer and closer to a particular number?

b) Keep on changing without pattern?

In either case can you say more?

I have just published a (rather long) article on mathematical surfaces, their models and links to art over at Maxwell’s Demon.  Here is a sneak preview.

Minimal Möbius, Benjamin Storch

Edmund Harriss, sometime contributor to the Math Factor, makes his first appearance in this early segment, from February 29, 2004.

Standard Podcast Play Now | Play in Popup | Download

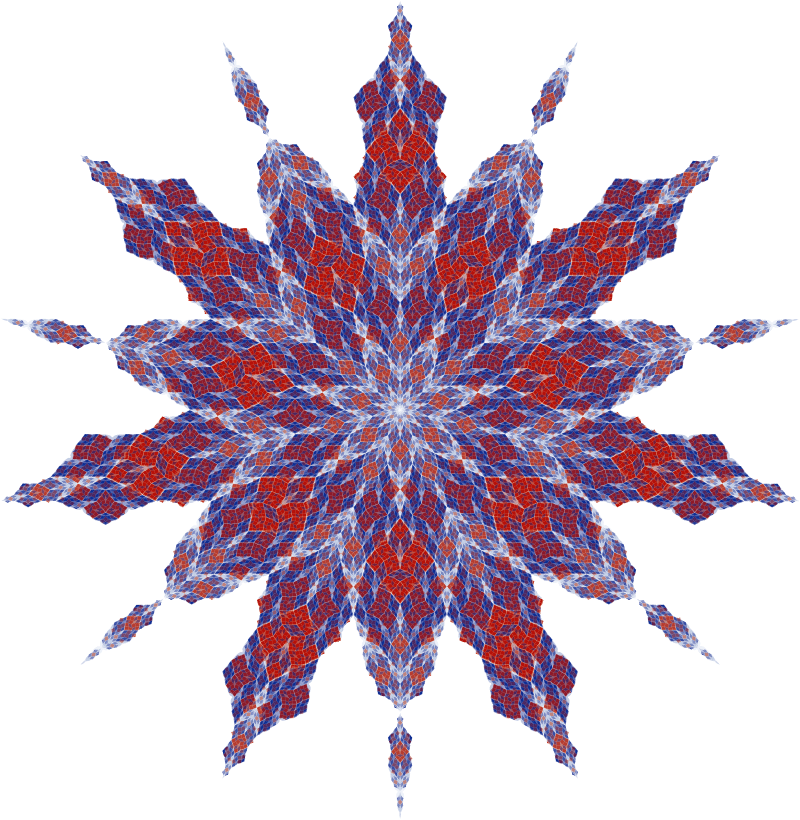
Greetings mathfactorisers!  I am one of the new wave of additional commentators on the website.  I thought I would introduce myself a little.  I am currently working as a postdoc researcher at Imperial College London, though I am also polishing my CV as my current contract finished in March.  My research is in tilings and patterns, especially those which fit onto themselves at different scales.  For those of you in London next summer I am preparing an exhibit titled “How shapes fill space” for the Royal Society Summer exhibition.  This will look at the mathematics of tilings and patterns with lots of shapes and models to play with.I also like to make pretty pictures from this research, like the example below, which is based on a tiling created by the prime mathfactor Chaim himself.   I hope to describe some of this on the mathfactor, for a taste check out my other writing at Maxwell’s demon.  This piece on rep-tiles is probably of particular interest.  For more of my pictures take a look at my website.