HK. Spiders and Fly
Another pursuit puzzle:
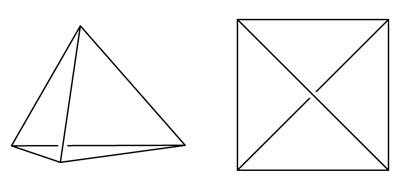
Three crazed, robotic professors (or, if you prefer, “spiders”) try to chase down a psychic, but slightly faster student (the “fly”) along the edges of a tetrahedron. It’s easier, perhaps, to draw it out in the view at right below.
Is there a strategy that allows the professors to catch their prey?
Wait a sec– did we say the prey is SLOWER? Obviously one fast hunter can chase down slower prey, even if the prey knows exactly what’s coming…
Wait another sec– isn’t the point that the professors are morons and robotic? Maybe we DID state the puzzle correctly.
Long time listeners know it wouldn’t be the first time we’d inadvertently added a “meta-puzzle”, namely, to figure out what it is we’d meant to say!! Thanks Byon for pointing that out!
(PS Don’t forget the spoiler tag if you post spoilers in the comments!)
(PPS Apologies: our policy of holding back solutions sometimes gets the order of the comments pretty scrambled)

 mathbun.com
mathbun.com
Byon said,
February 3, 2012 at 11:31 am
Maybe I’ve missed something, but…
[spoiler] The profs start on any 3 of the 4 vertices. If the student is on one of the 3 edges surrounded by a prof, she is caught. If not, one prof walks directly to the last vertex, and the student must be trapped on one of the last 2 edges.
The 2D tetrahedron made it pretty easy to visualize. Perhaps it’s better without it.
[/spoiler]
Byon said,
February 3, 2012 at 11:32 am
Oh, and didn’t you mean “slightly FASTER student”?
strauss said,
February 4, 2012 at 11:27 am
I may be missing myself something in Byon’s comment, but I don’t think that will work– as the profs move to get the student (that’s funny– I was imagining a slouchy guy) they have to open up one of the routes up to the top, but then…
Byon said,
February 6, 2012 at 8:52 pm
Consider the left image of a tetrahedron, with 3 vertices low, and 1 high.
[spoiler]Just have the 3 profs walk to the bottom 3 verts. Now the student must either be on one of the 3 bottom edges, in which case she is surrounded by 2 profs with no escape, or she is on one of the top 3 edges. If she is on a top one, all 3 profs just start moving up to the top vert, and she has no escape. Or just one can walk up, and she’ll have to go to the top vert if she isn’t already there, and then head down towards one of the waiting profs. Trapped again. [/spoiler]
Mark said,
February 8, 2012 at 5:58 am
I found a solution:
[spoiler]
assuming:
spiders don’t know where the spider is (so we have to make sure the fly cannot pass us)
spiders may meet and bypass each other
We start off with all spiders in one corner. Two spiders traverse the same egde, the second spider of those two traverses another adjacent edge. (see diagram below)
.
|
. _ .
These two edges and three corners cannot have a fly (or else it has been eaten). So the middle one now traverses the diagonal edge. This causes three edges to be free of the fly.
. .
| /
. _ .
Now we sacrifice an edge (either the left of bottom one). So one spider on the outside edge goes back to the bottom left and goes up the diagonal.
. .
| /
.
Then it connects the two upper vertices by traversing it’s edge, forming a triangle.
. _ .
| /
.
The only thing left is for all three spiders to simultaneously move into the invisited edges and cornering the fly in the last corner.
[/spoiler]
Mark said,
February 8, 2012 at 10:31 am
On second thought I found a flaw, was a bit too eager.
JP said,
February 8, 2012 at 8:36 pm
Byon is right if the professors can see the student. What if the tetrahedron is so large that they can not tell when he is on an edge between them?
Joe said,
February 9, 2012 at 2:55 pm
Byron, I’m guessing at the intent here, but I think what you’re missing is that the professors don’t know where the student is. That’s why they made a point of saying that the student is “psychic” and knows where the professors are. If you think of the professors as “blind” the puzzle might make more sense.
Maybe not though. I think that puzzle may be impossible.
Perhaps it’s blind professors and a *slower* student…
Byon said,
February 9, 2012 at 8:51 pm
Oh.. OK, thanks. No wonder it seemed too easy. :)
Stephen Morris said,
February 10, 2012 at 1:18 pm
I had also assumed the professors know where the student is, in which case Byon’s solution seems to work. But I think JP may be right, that the professors can’t see the student until they are upon him. This is the best I can do, I don’t know if it is the intended solution.
[spoiler]This method does not guarantee catching the student within a particular time but does guarantee catching them eventually. I assume that the psychic student knows where the professors are but not where they will go next. The three professors start on the top vertex and each takes a different edge so they end up on the three vertices on the base. The student must now be on one of the three edges on the base. I can’t see how to cover all three edges but I can cover two of them. This gives a 2/3 chance of catching the student whatever he does and the professors just repeat the process until they get lucky which they must do eventually. It requires some co-ordination between the professors which may be a problem. At random one of the professors moves along one of the base edges. There is a 1/3 chance that he finds the student. This professor, and the other professor on the same vertex, now walk to the third professor. There is a 1/3 chance that they catch the student. But now we are back at the starting position with all three professors on the same vertex. So the professors can execute the same strategy again, each time they have a 2/3 chance of catching the student. Assuming it takes 1 hour to cover an edge we can calculate how long we expect them to take, E = 1/3 x 2 hours + 1/3 x 3 hours + 1/3 x (3 + E) hours which solves to give E = 4 hours.[/spoiler]
Byon said,
February 10, 2012 at 6:23 pm
If the student is psychic, I would think that means she knows what the profs will do, even before they know, in which case I think she she can avoid them forever.
Daniel said,
February 17, 2012 at 12:10 am
I think the solution given on air actually indicates that the student is intended to be slower than the professors: [SPOILER]
The solution given was that one professor goes around the outside of the “square” (as per the diagram). The others go back and forth across the diagonals timing those motions to reach the corner at the same time the professor going around the outside reaches that corner.
Surely the student can simply stay directly opposite to the professor going around the outside, assuming that s/he actually is at least as fast as the professors. The student is then never caught by the professor going around the outside and since whenever s/he’s at a corner, the professor on the diagonal is at the opposite corner, s/he’s never caught by the other professors either.
That solution does work if the student is slower than the professors, since s/he can’t stay clear of the professor going around the square and is forced to move onto a diagonal. So I think that despite earlier disclaimers, the intended puzzle was in fact that the student be slower than the professors. If the professors can’t see the student, then being faster than the student doesn’t automatically mean that catching up is easy if there are multiple ways to escape. To take the analogy of the three cheetahs and the wildbeest- if the cheetahs are deaf and blind they don’t stand a chance of catching the wildebeest- there’s just too many ways it can go. [/SPOILER]
strauss said,
February 17, 2012 at 11:13 am
I may just chalk this one up as a loss…
Jack said,
November 26, 2012 at 9:02 am
I think I have a solution to the professor and student puzzle that doesn’t depend on the their relative speeds: [spoiler]The professors all start at the top vertex of the tetrahedron and move down along separate edges until each of them is at a different base vertex. If they haven’t caught the student by then, she must be on one of the base edges. Two of the professors then stay still while the third sweeps along one base edge, then back to his corner and along the second base edge. If she is still not caught, she must be on the third base edge, so the two other professors move towards each other[/spoiler]