That the worm falls off the end of the rope depends on the fact that the incredible
harmonic series

1 + 1/2 + 1/3 + 1/4 + . . .
diverges to infinity, growing as large as you please!

If you try adding terms up on a calculator, this scarcely seems possible! By the time you have added the hundredth term, you will have a reached only a whopping 5.187… (and each new term will be less than .01).

After adding up a million terms, you will have made it only to about 14.39272672… — and each new term will be less than .000001. Does the series really diverge?

The eighteenth century mathematician Jacob Bernoulli gave a very elegant proof that it does:

1/2 is at least 1/2

1/3 + 1/4 is at least 1/4 + 1/4 = 1/2

1/5 + 1/6 + 1/7 + 1/8 is at least 1/8 + 1/8 + 1/8 + 1/8 = 1/2

1/9 + . . . + 1/16 is at least 8 x 1/16 = 1/2

etc. So the result of adding up the first 2ⁿ terms 1/2 + 1/3 + . . . + 1/2ⁿ is at least n/2, and in particular, can be as large as we please.

But this does take a long time to get anywhere. To add up to, say, 100, Bernoulli’s proof shows us that 2¹⁹⁸ (about 4×10⁵⁹) terms will suffice. But maybe this is more than we actually need.

---

A basic fact from calculus is that the area under the curve y = 1/x, from x = 1 to x = N is exactly ln N.

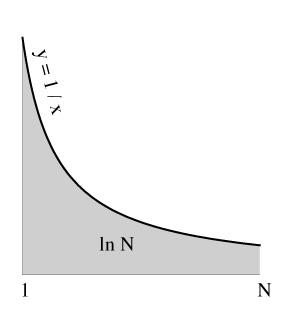
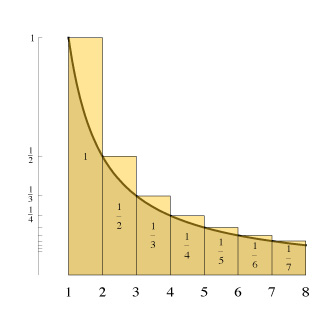
Now the area of a box 1 unit wide and 1/n units tall is 1/n, and boxes of width 1 and heights 1, 1/2, 1/3, . . . altogether have area 1 + 1/2 + 1/3 . . .

Here we see that these boxes can be arranged to show that

1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 > ln 8

Shifting the boxes over, we see that

1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 < ln 8

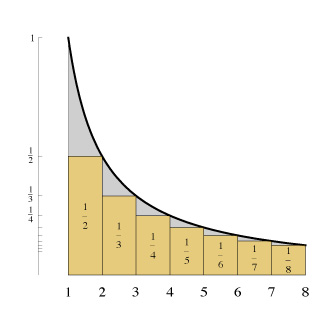
This gives us a much better bound on the harmonic series. Generally, we have that

1 + 1/2 + . . . + 1/n is between ln (n+1) and (ln n) + 1.

So to be sure that the series sums to at least 100, we can be sure that e^100-1 (about 2.7×10⁴³) terms will suffice!

---

The great Leonhard Euler proved that in fact, in the long run, 1 + . . . + 1/n tends to be exactly ln n plus a constant; Euler’s constant, usually denoted by γ (gamma), is about .577215664901…

So the sum of the first million terms is about (ln 1,000,000) + γ, and if we want to sum to 100, we need to have n such that ln n + γ is greater than 100; in other words, e ^{(100 – γ)} (about 1.5×10⁴³) terms will do.

---

The series Σ 1/(n ln n) diverges even more slowly still, taking about e^e^n terms to sum to n (!!) The series Σ 1/(n (ln n) (ln ln n)) takes e^e^e^n terms to sum to n. Etc!!