First, let’s answer last week’s puzzle on clocks!

As it turns out, there are 143 times in each twelve hour period for which you can switch the hands of a clock and still have a legitimate time! It’s easy to find these by plotting the positions of the hands throughout the day:

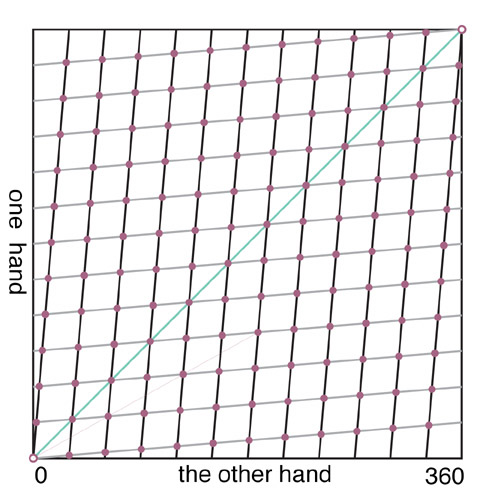
The darker lines show the positions of the hands if the vertical scale is for the minute hand and the horizontal scale is for the hour hand. The lighter lines reverse this. Where the lines meet, the position could make sense with either hand in either position.

If you count these intersections, you’ll see there are 143 times when the hands could be switched. The times on the green diagonal are when the two hands coincide– there are 11 of these, and the time is not ambigious since the time can be read in only one way. So there are 132 ambiguous moments. Hey– as Kyle asks, what is a better name for those special times of the day?

Here are some more of these:

.

And here are all 132!

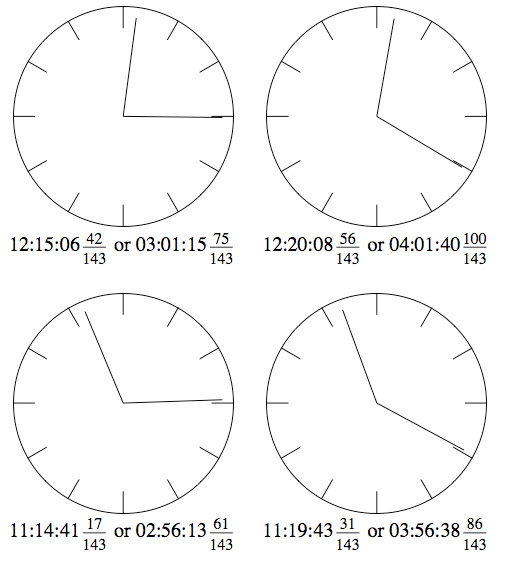
Ok, on to the next puzzle!

A set of numbers is perfectly summing if each of the numbers in it divides into the total. Can you always throw in some more numbers to a set to make it perfectly summing?

For example, {3,5} is not perfectly summing, but we can increase it to {3, 5, 10, 12, 30}; this is perfectly summing. Kyle asked about {4,9}– there is one solution with a total of 864; but uhm, this might not be optimal.

The real question is what is the general method? Try it out on {7,9,11}!

Standard Podcast [ 7:13 ] Play Now | Play in Popup | Download