In this segment, we give some explanation of how Benford’s Law actually arises in so many settings: why are so many kinds of data logarithmically distributed? And we give a surprising fact about runs of coin tosses, and a new puzzle. 

Standard Podcast Play Now | Play in Popup | Download

Standard Podcast Play Now | Play in Popup | Download

Benford’s Law is really quite amazing, at least at first glance: for a wide variety of kinds of data, about 30% of the numbers will begin with a 1, 17% with a 2, on down to just 5% beginning with a 9. Can you spot the fake list of populations of European countries?

 Looking at these lists we have a clue as to when and how Benford’s Law works. [spoiler]

In one of the lists, the populations are distributed more or less evenly in a linear scale; that is, there are about as many populations from 1 million to 2 million, as there are from 2 million to 3 million, 3 million to 4 million etc. (Well, actually the distribution isn’t quite linear,  because the fake data was made to look similar to the real data, and so has a few of its characteristics.)

The real list, like many other kinds of data, is distributed in a more exponential manner; that is, the populations grow exponentially (very slowly though) with about as many populations from 100,000 to 1,000,000; then 1,000,000 to 10,000,000; and 10,000,000 to 100,000,000. This is all pretty approximate, so you can’t take this precisely at face value, but you’ll see in the list of real data that, very roughly speaking, in any order of magnitude there are about as many populations as in any other– at least for a while. 

Data like this has a kind of “scale invariance”, especially if this kind of pattern holds over many orders of magnitude. What this means is that if we scale the data up or down, throwing out the outliers, it will look about the same as before. 

The key to Benford’s Law is this scale invariance. Data that has this property will automatically satisfy his rule. Why is this? If we plot such data on a linear scale it won’t be distributed uniformly but will be all stretched out, becoming sparser and sparser. But if we plot it on a logarithmic scale, (which you can think of as approximated by the number of digits in the data), then such data is smoothed out and evenly distributed. 

But presto! Look at how the leading digits are distributed on such a logarithmic scale!

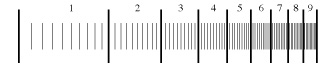
That’s mostly 1’s, a bit fewer 2’s, etc. on down to a much smaller proportion of 9’s.

[/spoiler]

This is the solution to Morris: Trial/Trual/Whatever.  Please look there before reading the solution.

It turns out the right word is truel, first coined in 1954 by Martin Shubik.

Read the rest of this entry »

I’m overdue to post a puzzle, but I’m momentarily tapped out. Here’s a curiosity in the meantime: You can provide a very good estimate of a conversion from miles to kilometers by choosing sequential Fibonacci numbers.  The conversion rate is 1.609344 kilometers to a mile. So this gives us:

This leaves you in pretty good shape if you need to get from Cincinnati, OH to Destin, FL at 610 Miles, but what if you need to convert some distance that doesn’t happen to be a Fibonacci number?  Just build it up from parts!

100 miles is 89+8+3.  So in kilometers, that’s 144 + 13 + 5 or 162 kilometers.  (160.9344 by conversion…)

OK.  Here’s a puzzle, sort of.  I found this interesting set of numbers recently:

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 53, 371, 5141, 99481 }

The series doesn’t continue.  That’s all of them.  What’s special about those numbers?

Mrs Smith has two children.  The eldest is a boy.  What is the chance that both are boys?

Mrs Jones has two children.  One is a boy.  What is the chance that both are boys?

Mrs Brown has two children.  One is a boy born on a Tuesday.  What is the chance that both are boys?

From Gary Foshee published on Ed Pegg’s http://www.mathpuzzle.com/ 

When two men get up ridiculously early to fire pistols at each other we call it a duel. Personally I prefer to lie in.

But what is the right term when three men skip breakfast to fire pistols at each other?

In a cold, misty field near the outskirts of Paris the sun peers over the horizon to see three men face each other with pistols.  Xavier is an expert shot, he never misses. Jean-Christophe is a very good shot, he will get you four times out of five. Francois only has a fifty/fifity chance of hitting his target.

They each take turns to fire their pistol.  

What is the best strategy for each of them and what odds would you give for the last man standing?

After the bodies had been cleared away I started to wander home only to hear the referee say ‘Maintenant, M. Galois et ami’

No, we are not kidding about the gravity of the extraneous zero problem. We must speak out now, before the end of the decade and attention fades.

Standard Podcast Play Now | Play in Popup | Download

In Living With Crazy Buttocks, Stephen Morris told us of a rather interesting party. The story continues…

After winning their trip to Paris, the guests became elated and celebrated with the consumption of some adult beverages. Ever responsible, the host confiscated the keys to all cars to ensure that no one drove home drunk. Later on, when things started to calm down, party-goers started to request the return of their keys claiming to be sober enough for the drive home.

Having once been out-done by the guests, our host took another whack. He distributed all of the keys, but did so randomly. He then presented a challenge he felt sure they’d only be able to satisfy if they were indeed sober enough to drive. They were allowed to exchange keys, but only in rounds. During each round, each party-goer could either do nothing or pair up with another party-goer and exchange the sets of keys each was holding. (Each party-goer could be part of at most one pairing per round.) No one would be allowed to drive home unless everyone recovered their own keys.

The host wished to allow only a fixed number of rounds. To be fair, he wanted to be sure that it would indeed be possible to make the change. However, he also wanted to make it as difficult as possible for the party-goers. What is the minimum number of rounds must allow them to ensure that an exchange would be possible?

For clarity, all key recipients can discuss, share information such as who has the keys of whom, and agree upon a strategy. Also, careful readers will realize that there were 20 guests at the party originally. Sadly, it was a rather disorderly party and some guests did leave early, but many more appeared. Everyone present at the key ceremony had a key confiscated, and everyone with a key confiscated received a key for this challenge, but neither you nor the host knows just how many there are.

{ Hi, Steve here. Jeff asked me to post a solution and I’m more than happy to oblige. It’s a fun puzzle with some nice maths to explore. I learnt a lot about graph theory and a new theorem (new to me), Turan’s theorem. More on that later. }

In Yoak: Batteries, and the Problem-of-the Week Jeff posed a great problem from Stan Wagon’s Problem of the Week.

You have eight batteries, four good and four dead. You need two good batteries to work the device; if either battery is dead then the device shows no sign of life. How many tests using two batteries do you need to make the device work?

Read the rest of this entry »

Here’s an idea for a general tiling game. Start with a set of shapes and 2 (or more) people. Each person takes it in turn to place onto a patch of tiling. The winner is the last person to move.

So here’s the puzzle:

Take the Myer’s polyhex tile:

Can you:

1. Find rules to avoid easy draws (for example wandering off in one direction to infinity).
2. Find a winning strategy?

I personally have no idea, so this is a challenge problem!

If you have access to a Laser Cutter or other fancy computer device the cut files are on Thingiverse.