When I became chairman of my department a few years ago, I moved from my office far down at the end of the hall to one much closer to the center of action: the tea room! I make a lot more visits there than I used to, and began to notice a frustrating pattern:

Far more often than seems reasonable, there’s not even a full cup of coffee in the coffee pot! Once again, someone has left a nearly empty pot with no regard to the next person (me, whine)!

This seems to happen so often I began to wonder what kind of boors I’ve been working with all these years. They seem like nice people and all, but…?

And then I realized: there’s a perfectly logical reason, a mathfactor puzzle, if you will, that explains this phenomenon perfectly, no boors required, no special tricks, just sensible activity by all. My faith in my colleagues has been restored.

Why is it that on average I see an emptier rather than fuller coffee pot?

PS let us know what works for when we return…

Greg Chaitin, author most recently of MetaMath!,  discusses the ubiquity of undecidability: incredibly all kinds of mathematical and physical systems exhibit utterly unpredictable, baffling behavior– and it’s possible to prove we can never fully understand why!

Standard Podcast [ 1:02:19 ] Play Now | Play in Popup | Download

Quick interviews with folks here at the Gathering For Gardner, including Stephen Wolfram, Will Shortz,  Dale Seymour, John Conway and many others. 

Report From The Gathering For Gardner [ 18:58 ] Play Now | Play in Popup | Download

Standard Podcast Play Now | Play in Popup | Download

Benford’s Law is really quite amazing, at least at first glance: for a wide variety of kinds of data, about 30% of the numbers will begin with a 1, 17% with a 2, on down to just 5% beginning with a 9. Can you spot the fake list of populations of European countries?

 Looking at these lists we have a clue as to when and how Benford’s Law works. [spoiler]

In one of the lists, the populations are distributed more or less evenly in a linear scale; that is, there are about as many populations from 1 million to 2 million, as there are from 2 million to 3 million, 3 million to 4 million etc. (Well, actually the distribution isn’t quite linear,  because the fake data was made to look similar to the real data, and so has a few of its characteristics.)

The real list, like many other kinds of data, is distributed in a more exponential manner; that is, the populations grow exponentially (very slowly though) with about as many populations from 100,000 to 1,000,000; then 1,000,000 to 10,000,000; and 10,000,000 to 100,000,000. This is all pretty approximate, so you can’t take this precisely at face value, but you’ll see in the list of real data that, very roughly speaking, in any order of magnitude there are about as many populations as in any other– at least for a while. 

Data like this has a kind of “scale invariance”, especially if this kind of pattern holds over many orders of magnitude. What this means is that if we scale the data up or down, throwing out the outliers, it will look about the same as before. 

The key to Benford’s Law is this scale invariance. Data that has this property will automatically satisfy his rule. Why is this? If we plot such data on a linear scale it won’t be distributed uniformly but will be all stretched out, becoming sparser and sparser. But if we plot it on a logarithmic scale, (which you can think of as approximated by the number of digits in the data), then such data is smoothed out and evenly distributed. 

But presto! Look at how the leading digits are distributed on such a logarithmic scale!

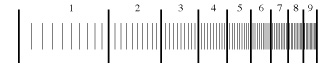
That’s mostly 1’s, a bit fewer 2’s, etc. on down to a much smaller proportion of 9’s.

[/spoiler]

In working out the proof for World of Britain I came across a paradox.  Maybe smarter Math Factorites can help me out?  My sanity could depend on it.

In the puzzle you have five different tasks.  On each day one of these tasks is given at random.  How long do you expect it to take to get all five tasks?

First consider a simple case.  Suppose some event has a probability, p, of happening on any one day.  Let’s say that E(p) is the expected number of days we have to wait for the event to happen.  For example if p=1 then the event is guaranteed to happen every day and so E(p)=1.

How can we calculate E(p)? 

Read the rest of this entry »

David Singmaster, Puzzler Extraordinaire, early master of the Rubik’s Cube, poser of the Singmaster Conjecture, etc, etc, engages in some wordplay.

Standard Podcast [ 11:34 ] Play Now | Play in Popup | Download

Chris S. writes:

I was wondering what is the theoretical ‘area’ of contact between two spheres in contact with each other. I was unfortunately not able to locate much (if any) information on this. After some thought into this I’ve realised that the spheres would meet at a single ‘point’ however what would the area of this ‘point’ be? The only source related to this claimed the area of contact, the point, has no area. How can a point have no area? If the spheres touch, musn’t there be an area shared between them? Even if only one atom?

Hi, the issue here is that there is a vast difference between physical, real things and the mathematical ideas that model them.

Real, mathematical spheres don’t exist, plain and simple! Never could, even as a region of space— space itself has a granularity (apparently) at a scale of about 10^-33 meters. There simply cannot exist a perfectly spherical region in physical space, much less a perfectly spherical body.

But as an abstraction, the idea of a sphere is very useful: lots of things, quite evidently, are spherical for all practical purposes.

For that matter, “points” don’t exist either, and are also a mathematical abstraction. (So, too, is “area”. Real things are rough, bumpy and not at all like continuous surfaces, on a fine enough scale) But again, these _ideas_ are very good at getting at something important about lots and lots of physical things, and so have proved useful.

Tangent spheres do indeed meet in a single point, which has no area.

Spherical things meet in some other, messier way.

Hope this helps!

That the worm falls off the end of the rope depends on the fact that the incredible
harmonic series

1 + 1/2 + 1/3 + 1/4 + . . .
diverges to infinity, growing as large as you please!

Read the rest of this entry »

Standard Podcast [ 6:10 ] Play Now | Play in Popup | Download

Dana Richards, editor of The Colossal Book of Short Puzzles and Problems discusses the amazing Martin Gardner and his legacy!

Standard Podcast [ 8:37 ] Play Now | Play in Popup | Download

Faster than an exponential! More powerful than double factorials!! The Busy Beaver Function tops anything that could ever be computed– and we mean ever