Follow Up: Sequences of Averages
In response to the post “Stacking Cannonballs” Trevor H. writes:
I was very intrigued by the recursive sequence you mentioned in the past two episodes–the sequence that begins with 1 and each successive term is the average of all the previous terms times some constant. I have always been fascinated by Pascal’s triangle and all of its surprise appearances in mathematics. Also, my fist encounter with doing mathematics for fun out of my own curiosity was to find a formula for triangle numbers. Like Kyle, I was inspired by bowling pin arrangements. The experience was very rewarding and I have been in love with mathematics ever since.
As you mention in the episode “Stacking Cannonballs,” it is easy to show what the sequence evaluates to through algebra but it is not easy to see what is really going on. This is a view I rarely hear mentioned by math people but I have held to be fundamentally important. It seems to me that geometrical interpretations always shed more light than algebra. Because of the nature of the sequences constructed from this recurrence, I felt there must be a geometric way to look at this problem.
Let us represent numbers by pennies as you suggest on the show. The first case is trivial and does not offer much insight, so we can start by looking at the case with constant k := 2. On the show, you added the terms, took the average, and then multiplied by the constant. I suggest we sum the terms, multiply by the constant, and then take the average because 1) we can and 2) we do not have to think about fractional pennies.
The first two terms are 1 and 2. The next term is found by adding these together. Geometrically, we are adding consecutive numbers together which gives us a triangle number. Multiply this by 2 and arrange as follows:
. \. . . .\ .This makes two rows, which conveniently is what needs divided by to give us the average. Look at one row to get the next number: 3. Consider a few more terms written in this way:
. \. . . . . \ . . . . .\ . . \. . . . . . \ . . . . . . \ . . . . . .\ . . \. . . . . . . \ . . . . . . . \ . . . . . . . \ . . . . . . .\ .In each case, we have as many rows as we need to divide by to find the average. Thus we always read across a row to find the next term (all rows sum to the same number). Notice geometrically that the next term is a “vertex” plus an “edge.” This becomes a pattern once we get to later sequences.
Suppose we let the constant k:=3. This generates the sequence of triangle numbers. For each term we sum all the previous triangle numbers, multiply by three and then find the average. The sum of triangle numbers is a tetrahedral number, so let us interpret the sum this way. This is hard to draw with periods via email, but try to image arranging three tetrahedrons in a similar way to the triangles so that we get a three dimensional figure where each plane (instead of row) has the same number of points and the number of planes equals the number of triangle summed. Geometrically, the way to arrange these tetrahedrons is to set the first one flat on the table with one of its faces. Place the next one on an edge. Balance the third one on a vertex. This arrangement will give you an equal number of points on each plane. Thus, summing one plane is our next term. Looking at either the top or bottom plane, notice that this sum is a “face” + “edge” + “vertex”. Although I am unable to visualize the fourth dimension, I image this pattern will continue. Since we would then be multiplying by 4, place one hyper-tetrahedron on a tetrahedral side, one on a triangular face, one on an edge, and one on a vertex. This should divide the total in a convenient number of spaces each with the same number of vertices.
I like this interpretation because the constant represents the dimension we are looking at and the division represents the number of equally distributed levels and the terms of the sequence represent generalizations of the triangle. Sorry this email ran long. I hope this helps you see the sequences in a new way.
This was a very stimulating email!
Here’s a way to reinterpret the 3-D case Trevor discusses:
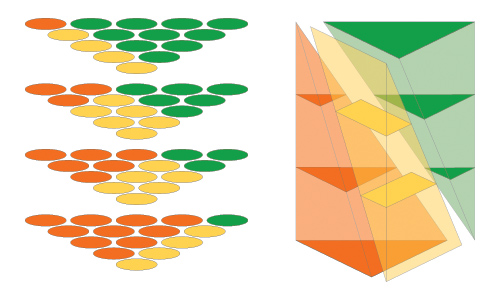
And indeed, his observation that the pattern should continue is correct. Here’s a typical slice of the 4-D case:

As the “movie” progresses, the little green tetrahedron grows and the orange tetrahedron shrinks; the blue triangular prism widens, and becoming flatter and shorter, and conversely, the green prism becomes longer and narrower.
Is this simpler than the algebra? I don’t think so, really, but it is a neat way to look at things!
I should add a comment about the general case; I think it’s clear from Trevor’s note that he sees how this works, but let’s be explicit: in general, one is chopping up a (k+1)-dimensional prism with k-dimensional tetrahedra as cross-sections. (The movie frame above is one of these cross-sections in the 4-dimensional prism.) The prism, and each slice, is divided into (k+1) tetrahedra, in various reposes. In fact, for each i from 0 to k, there’s a tetrahedron with an i-dimensional facet on the bottom of the prism, and a (k-i) dimensional facet on the top. For example, in the 3-dimensional prism, shown in the first figure, the three tetras are “triangle down” (a two dimensional facet on the bottom of the prism), “edge down” (a one dimensional facet down) and “point down” (a zero dimensional facet down) As we move up, all the roles swap.
 mathbun.com
mathbun.com