It’s been a few months now since we’ve posted any new podcasts, and  from the many weepy emails asking when, oh when will the mathfactor podcast return, we know we’ve been missed — we’re really grateful that we have so many avid listeners! In the meantime, Stephen Morris has been holding down the fort with many excellent posts here on the site, as you probably know if you’re reading this here. Great work Stephen!

I thought I’d take a moment to share what’s been shaking round here and where things might be going. First off, I have to say, really, it has been nice taking a break from the podcast. After all, we’ve been doing mathfactor pieces steadily for six years! (Still have about 70 early radio segments to post, I think) But I know we’ll get back to it someday, maybe someday pretty soon. Ideas are certainly starting to pile up again…

In my own work, things are going great. Our new course, Mathematical Thought, is chugging along nicely in its second year, with our long-time correspondent Edmund Harriss and colleague Janet Woodland at the helm. This course is really quite radical in its way—students must take significant initiative to succeed, but are free to approach whatever mathematical ideas they want to, in a way that plays to whatever their expertise or interests are. So far, it’s working.

Meanwhile, I’m now teaching geometry for future teachers; I should have done this years ago—it’s obviously the most effective way to have a significant local impact on the culture of mathematics. The students are deep in the midst of wrastling with how to develop and communicate fun mathematical ideas in their classrooms, and the results seem promising.

Some careful listeners may have picked up that I’m now chair of my department, and in that role I’ve been working hard at infusing the place with the sensibility the Math Factor exemplifies:

Serious intellectual engagement is fun, expected of everyone, open-ended into a lifetime.

As happens, our college is in the midst of a major reassessment of our core curriculum, and we have a chance to work in that direction, producing a truly visionary core that will fully model these high ideals. The outgoing dean’s request for innovative course proposals was met by a resounding burst of energy and creativity and it seems we are poised for a really interesting and exciting period here. 

So, when will the Math Factor podcast come back? We’ll see what happens in the next few months, but if all goes we might hope for, I may be in a position to foster a lot more of this kind of fun!

Ciao for now, Chaim

If you are anything like me, and I hope for your sake that you aren’t, then you will often ask yourselves questions such as:

    Late at night, when they’re peckish, do Vampires ever bite themselves?

    Was Hitler’s moustache homage to Charlie Chaplin?

    Can I find an exact formula for the Fibonacci sequence?

I can only answer one question. Which one?  

Yup, it’s the last one.

In Yoak: Miles, Kilometers and Fibonacci Numbers Jeff showed a lot of fun stuff about the Fibonacci sequence and how it relates to the golden ratio. He didn’t explain how this comes about.

The Golden Ratio, phi (I’ll use g), was beloved by classical architects and is still loved today. It was thought to be the most aesthetically pleasing ratio. It was the ratio used for the Parthenon.

It has a simple definition, if you have a rectangle with proportions 1:g then you can remove a square from one end and the leftover is a rectangle with the same proportions.

From that you can work out that g² = g + 1 and g = 1 + 1/g. There is a revealing symmetry in that last equation which is better shown by g – 1/g = 1, if you switch the sign and invert g then you get another solution. 

Anyway:

    g = (sqrt(5) + 1)/2 ~= 1.618

    1/g= (sqrt(5) – 1)/2 ~= 0.618

The Fibonacci sequence goes 1, 1, 2, 3, 5, 8, 13, 21, 34 …

The Fibonacci rule is F_n+2 = F_n+1 + F_n

There are lots of sequences that fit this rule. Any particular sequence is fixed by specifying two elements, for example the actual Fibonacci sequence starts 1, 1. Another sequence that fits the rule is 1, 3, 4, 7, 11, 18, 29 …

We note that if xⁿ⁺² = xⁿ⁺¹ + xⁿ then the sequence 1, x, x², x³, x⁴ … satisfies the Fibonacci rule.

We can solve for x. Dividing by xⁿ and rearranging gives x² – x – 1 = 0.

This gives two solutions for x:

        g =                      (1+sqrt(5))/2

       (-1/g) = (1-g) = (1-sqrt(5))/2

Both of these solutions for x generate sequences that satisfy the Fibonacci rule.

    1, g, g², g³ …

    1, (1-g), (1-g)², (1-g)³ …

But we can go further. Put X_n = Agⁿ + B(1-g)ⁿ  then X_n satisfies the Fibonacci rule.

    A + B, Ag + B(1-g), Ag² + B(1-g)², Ag³ + B(1-g)³ …

A particular sequence that satisfies the Fibonacci rule is fixed by just two entries. I claim that we can always find values for A and B that will create any sequence which satisfies the Fibonacci rule.

We have two simultaneous equations with two unknowns, A and B. This always gives a unique solution (it matters that (1, g) and (1, 1-g) are linearly independent vectors). For example lets calculate A and B for the actual Fibonacci sequence. F₁ =1 and F₂ = 1. Using the Fibonacci rule backwards gives F₀ = 0.

So     F₀ = A + B = 0      F₁ = Ag + B(1-g) = 1

Working this through

    B = -A

    Ag – A(1-g) = 1

    A(2g -1) = 1

    A(2(sqrt(5) + 1)/2 -1) = 1

    A = 1/sqrt(5)

Which solves to give A = 1/sqrt(5), B = -1/sqrt(5)  

So we have : F_n = (gⁿ – (1-g)ⁿ) /sqrt(5)

Now there is something very bizarre going on here. We know that the Fibonacci sequence is a sequence of integers. We have found that it has an exact formula but the formula involves lots of irrational numbers, raising them to powers, adding and dividing them. Somehow this process always ends up with an integer. Knowing that we will always get an integer we can short-circuit the calculation.

Note that 1/ sqrt(5) is about 0.447, (1-g)/ sqrt(5) is about -0.276 and that (1-g)ⁿ/ sqrt(5) always has a magnitude of less than a half. Knowing that we will always get an integer we can just ignore this term and round to the nearest integer.

    F_n = round(gⁿ /sqrt(5)) for n >= 0

It is also true that

    F_-n = (-1)ⁿ⁺¹round(gⁿ /sqrt(5)) for n >= 0

To see this remember that 1-g = -1/g so F_n = (gⁿ – (-1/g)ⁿ) /sqrt(5). For negative n it is the first term that is smaller than a half and can be ignored. I’ll let you work out the rest.

In fact extending the Fibonacci sequence backwards gives … -3, 2, -1, 1, 0, 1, 1, 2, 3 …

What is most wonderful about this is that the ratio between successive members of the Fibonacci sequence is about g. It becomes very close very quickly. Also wonderful is that this technique extends to other sequences which are defined by similar rules. In general you can find an exact formula, involving taking powers of irrational numbers, which will always give you the integer you were looking for.

I find that quite amazing!

It shows that you cannot take one part of mathematics in isolation, if you want to understand integers you have to understand irrational numbers, and for many sequences complex numbers. It’s all interconnected, you can’t pick and choose. Even the simplest parts of mathematics are tied up in the most complex!

All good fun though!

It was very sad to hear that Benoit Mandelbrot has died aged 85.

He is one of very few mathematicians who has both changed the subject and captured the public imagination.  His high idea, that there is a symmetry across scales, is easy to understand especially if you have walked the coast of Britain. 

However it is the images that have really caught the imagination.  This one was iconic in the eighties.  Everyone knew this image, whatever age they were.  

It was also inspirational for a teenager interested in mathematics.

And most people understood the basic idea.  They could see the symmetries, how the main shape was repeated throughout the image on different scales.

This image was already iconic then.  But now we have so much more.  I was struck by this 3D fly-through:

I’m looking forward to putting on my virtual reality helmet and flying through these things, changing scales as I go.

Let’s leave the last word to Benoit Mandelbrot recorded at TED this year.

In Golden Earring – Radar Love I had a big problem.

This the solution so please read the problem first and have a go at solving it yourself.

My wife has lost a golden earring, I can buy a bunch of similar earrings but I know one is a fake.

I can weigh two groups of earrings, each weighing can give one of three results: they weigh the same; the left group is heavier, the right group is heavier.

The question is – how many earrings can be in the bunch I buy and leave me confident that I can find the fake with just three weighings?

Read the rest of this entry »

Smart shows have smart writers, and none are smarter than the writers of Futurama.  We’ve seen a number of clever math references in Futurama and the Simpsons.  Now a fully fledged theorem is written up on screen.

If I had a TV show that’s exactly what I would do.  As it is I just post on Math Factor.

The theorem is by staffer and Math PhD Ken Keeler.  In the show Harlem Globetrotter, and all-round genius, Sweet Clyde comes up with a theorem to solve an apparantly intractible problem.

To quote Professor Farsnworth ‘Who says pure maths isn’t useful in the real world!’

Professor Farnsworth invents a mind-switching machine.  A lot of plot later nine people have their minds in the wrong bodies.  Unfortunatley the machine has a limitation, it cannot process the same two bodies twice.

There seems to be no way out until Clyde and EthanTate enter.  Clyde comes up with ‘Sweet Clyde’s Inversion Theorem’ and saves the day.

He shows that however many people there are, and however mixed up their minds, it is always possible to get every mind back in the right body as long as you have two extra bodies to help, and you know your maths!

This is the mess they are in:

Fry’s mind is in Zoidberg’s body

Professor’s mind is in Bender’s body

Bucket’s mind is in Amy’s body

Leela’s mind is in Professor’s body

Emporer’s mind is in Bucket’s body

Hermies’ mind is in Leela’s body

Zoidberg’s body is in Fry’s body

Bender’s mind is in Emperor’s body

Amy’s mind is in Hermies’ body

Take a moment to solve this yourselves.  Remember you need to get each mind back in the right body by repeatedly switching the minds of two bodies.  No switch can be repeated.  You cannot switch two of the original nine bodies because we have lost track and assume those combinations have already been used.  So every switch must involve Clyde and/or Ethan.  

Read on for the solution.

Read the rest of this entry »

Trauma at home; my wife has just lost one of her golden earnings.  Fortunately I know someone who will sell me a bunch of similar earrings, for a price!

I know that one of his earrings is fake, but that’s okay because I can work out which one, replace my wife’s earring and still make a profit. 

I will have to bring out my earring weighing machine, the Radar Love, which lets me compare two groups of earrings and tells me whether one group is heavier or lighter than the other, or whether they are the same wieght.  This is the only clue I will get.

The Radar Love only has three charges.  At most how many earrings can I have bought and still be confident that I will find the fake?

Can you find a general formula for a given number of charges?

“There is a crack in everything, that’s how the light gets in” Leonard Cohen, ‘Anthem’

It is the things that don’t make sense that teach us the most.  

If you want to learn something new, start with something you don’t understand, something which doesn’t make sense.

However much you know there will always be chinks in your knowledge, chinks of light that may lead you to somewhere beautiful.

Consider this:

On a Sunday afternoon your prison guard tells you that he will conduct a surprise inspection at 10am over the next seven days.

You work out that he can’t wait until next Sunday, because then it wouldn’t be a surprise. 

So, could he do it on Saturday?

On which days would the inspection be a genuine surprise?

There is no consensus on this, which is why I describe it as a chink of light, a way to get at something deeper.  But what do you think?

In this special segment, John H. Conway reminisces on his long friendship and collaboration with Martin Gardner. 

Standard Podcast [ 57:24 ] Play Now | Play in Popup | Download

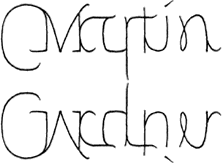Martin Gardner died this week.

One of his books is on my coffee table.  This is not a coincidence, there is always one of his books on my coffee table.

Many of my puzzles have come from these books.

I know him as the greatest collator and populiser of math puzzles, but of course his talents went far beyond this.

Rather than try to do my own second-rate obituary I will just point you at some links.

Scientific American, for whom he wrote for 25 years.  http://www.scientificamerican.com/report.cfm?id=Martin%20Gardner,%201914-2010

Make your own Martin Gardner Flexagons here, http://www.youtube.com/watch?v=4DETMhTC0H0.

The Daily Telegraph on his deconstruction of Lewis Carroll’s Alice books, http://www.telegraph.co.uk/news/obituaries/culture-obituaries/books-obituaries/7765184/Martin-Gardner.html

He wrote over 70 books.  Nothing I can say can begin to encompass his long and amazing life.  He is someone you need to discover for yourself.

He is already missed.

Greg Chaitin, author most recently of MetaMath!,  discusses the ubiquity of undecidability: incredibly all kinds of mathematical and physical systems exhibit utterly unpredictable, baffling behavior– and it’s possible to prove we can never fully understand why!

Standard Podcast [ 1:02:19 ] Play Now | Play in Popup | Download