Smart shows have smart writers, and none are smarter than the writers of Futurama.  We’ve seen a number of clever math references in Futurama and the Simpsons.  Now a fully fledged theorem is written up on screen.

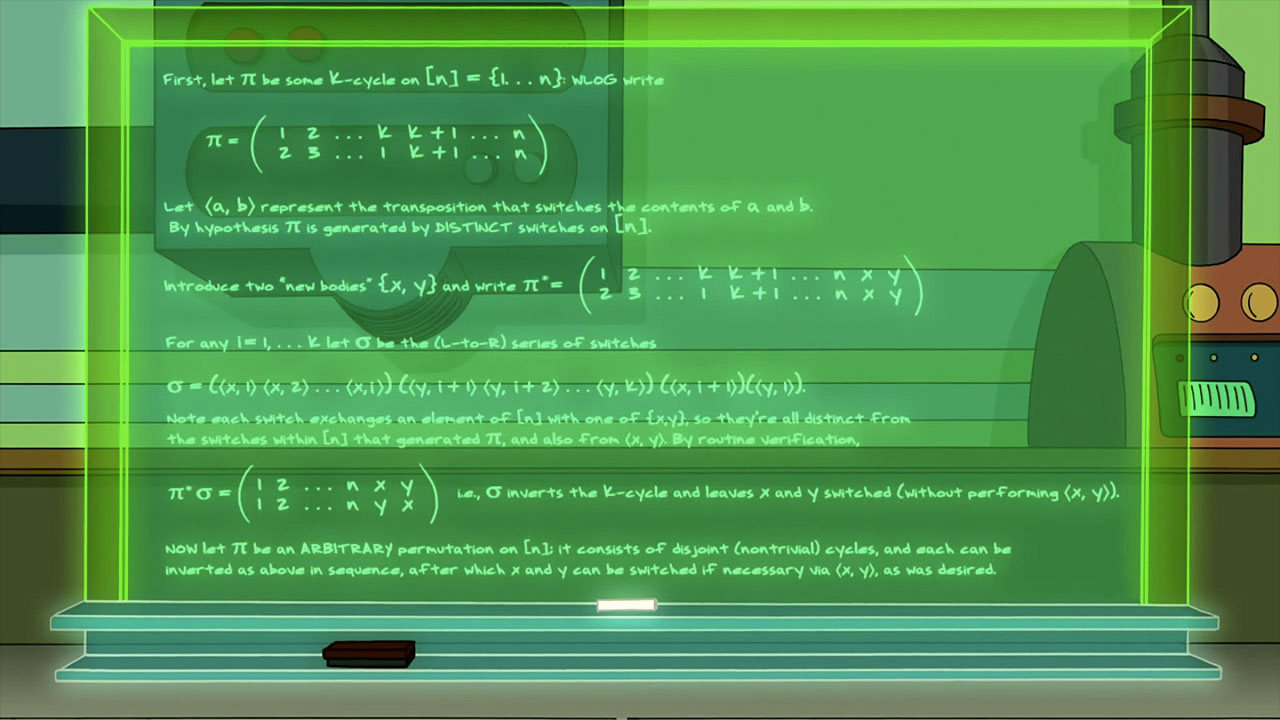
If I had a TV show that’s exactly what I would do.  As it is I just post on Math Factor.

The theorem is by staffer and Math PhD Ken Keeler.  In the show Harlem Globetrotter, and all-round genius, Sweet Clyde comes up with a theorem to solve an apparantly intractible problem.

To quote Professor Farsnworth ‘Who says pure maths isn’t useful in the real world!’

Professor Farnsworth invents a mind-switching machine.  A lot of plot later nine people have their minds in the wrong bodies.  Unfortunatley the machine has a limitation, it cannot process the same two bodies twice.

There seems to be no way out until Clyde and EthanTate enter.  Clyde comes up with ‘Sweet Clyde’s Inversion Theorem’ and saves the day.

He shows that however many people there are, and however mixed up their minds, it is always possible to get every mind back in the right body as long as you have two extra bodies to help, and you know your maths!

This is the mess they are in:

Fry’s mind is in Zoidberg’s body

Professor’s mind is in Bender’s body

Bucket’s mind is in Amy’s body

Leela’s mind is in Professor’s body

Emporer’s mind is in Bucket’s body

Hermies’ mind is in Leela’s body

Zoidberg’s body is in Fry’s body

Bender’s mind is in Emperor’s body

Amy’s mind is in Hermies’ body

Take a moment to solve this yourselves.  Remember you need to get each mind back in the right body by repeatedly switching the minds of two bodies.  No switch can be repeated.  You cannot switch two of the original nine bodies because we have lost track and assume those combinations have already been used.  So every switch must involve Clyde and/or Ethan.  

Read on for the solution.

Mathematically this is a permutation on nine elements.  Any such permutation consists of a number of disjoint cycles.  To see what I mean lets find the cycles here.

Starting with Fry’s body we find the matching mind is in Zoidberg.  So now we look for Zoidberg’s mind and find it in Fry.

So now we start with another character and follow the cycle which gives the following:

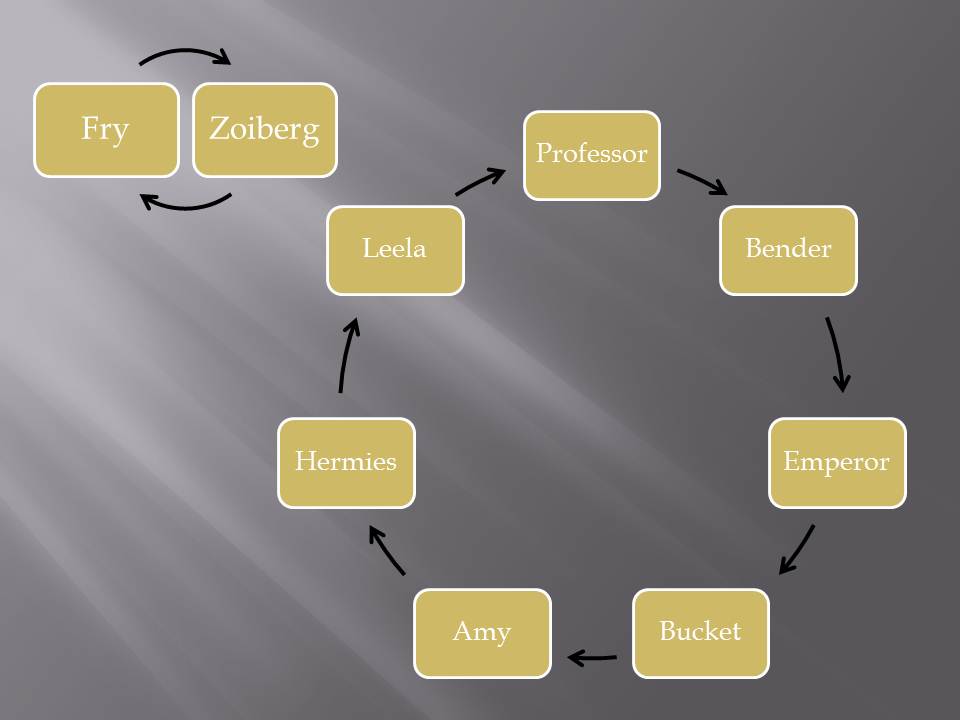
Fry and Zoidberg form a 2-cycle.  The other characters form a 7-cycle.

Enter Clyde and his basketball team-mate Ethan.

Clyde come’s up with’Sweet Clyde’s Inversion Theorem’ and saves the day.

We’ll get to that later but first lets see how  we unscramble this mess using Clyde and Ethans’ bodies as parking places for the mind.

Easiest to sort out are Fry and Zoidberg as they are only a 2-cycle.

We perform the following switches:

 

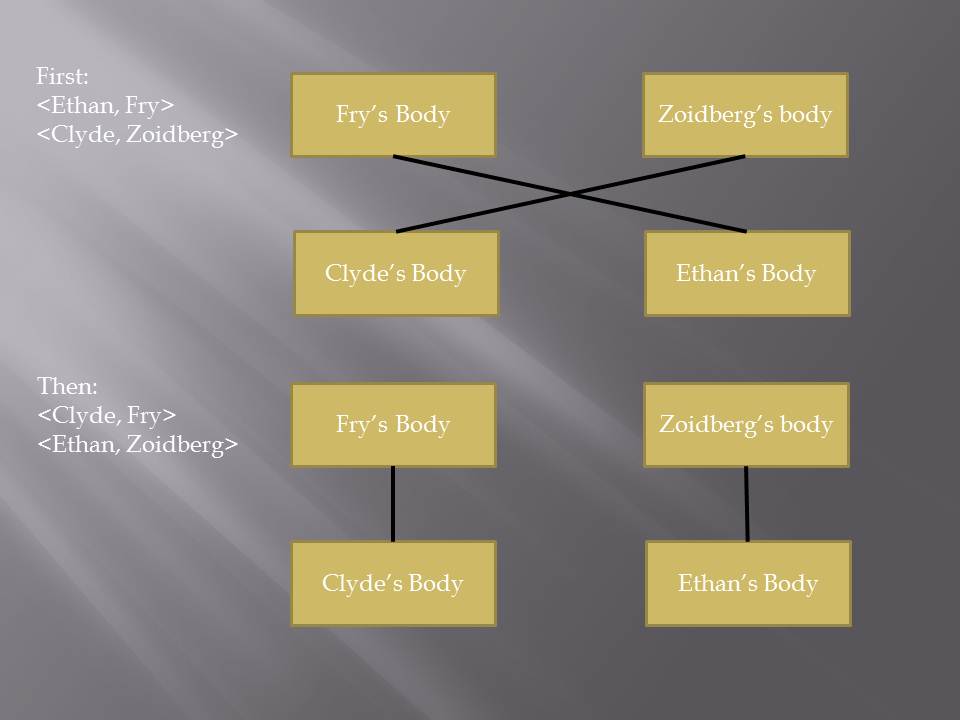
This switches Fry and Zoidberg but also switches Clyde and Ethan.  We could just switch Clyde and Ethan but first let’s sort out the other guys.

Hopefully it is clear that we did need two extra bodies to make this work.  We couldn’t have done it with just Clyde’s body.

We have sorted out a 2-cycle, now to sort out the 7-cycle.  This will be a bit tougher.

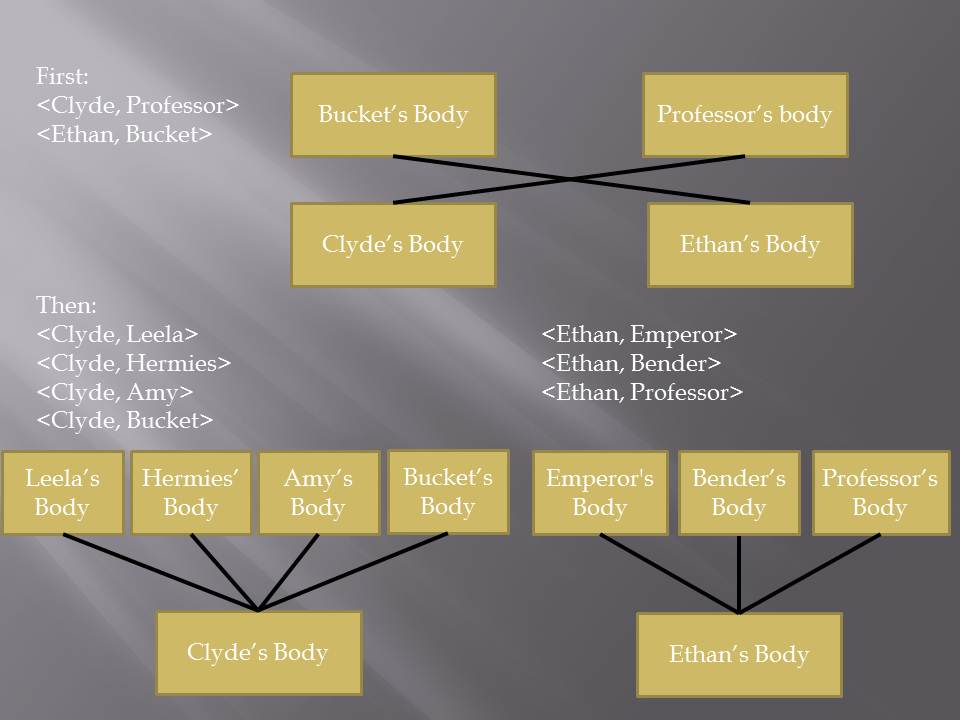
Let’s track what happens to the characters:

Bucket -> Ethan -> Emperor

Professor -> Clyde -> Leela

Leela -> Clyde -> Hermies

and so on.

All of the seven original characters end up in the right bodies. It reverses the 7-cycle that messed them up in the first place.

Clyde and Ethans’ minds are switched but this just reverses the switch that happened when we sorted out Fry and Zoidberg.  If it hadn’t we could still switch Clyde and Ethan.

Hopefully you can see we have used the same approach to sort out the 2-cycle and the 7-cycle.  In both cases we switch the two extra bodies (Clyde and Ethan) while sorting out the original characters.  This would work for any permutation, if we had more cycles we would just apply the same technique for each cycle.  If there were an odd number of cycles we would need to switch Clyde and Ethan at the end.

Now it’s time to explain ‘Sweet Clyde’s Inversion Theorem’

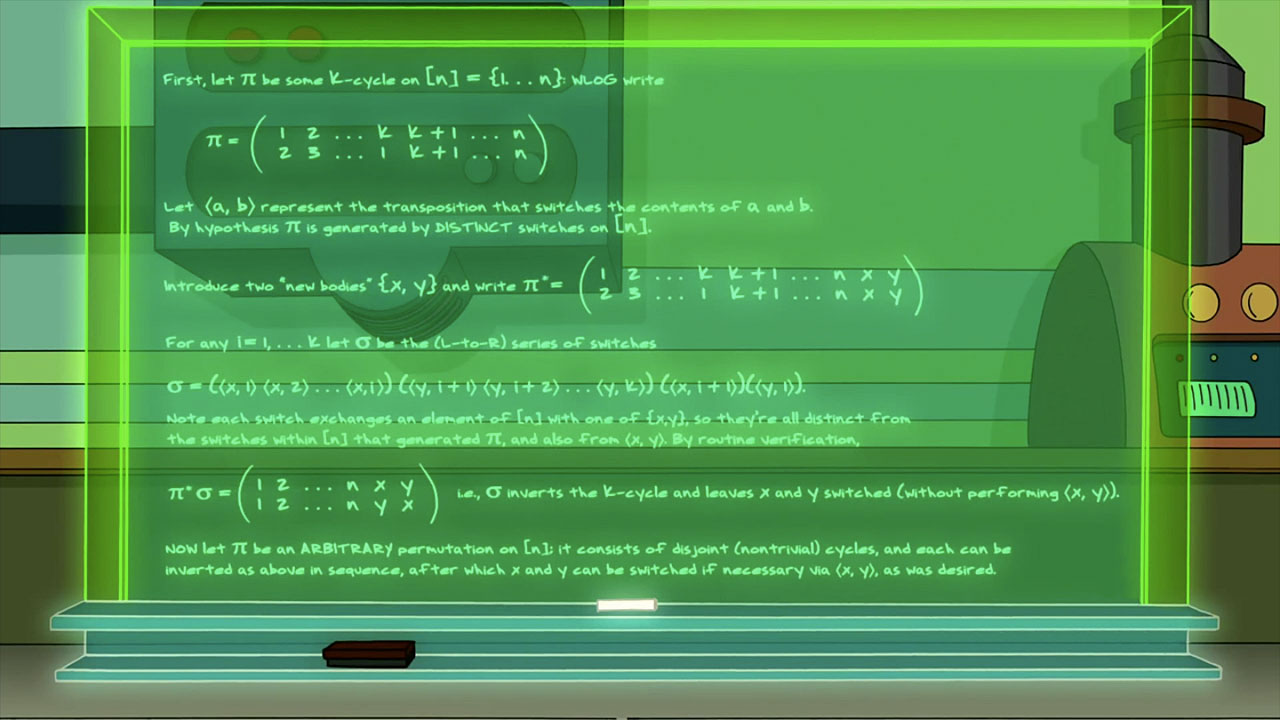
We need to introduce some notation.

For cycle’s we use round brackets so (a b c) means ‘move a to b, b to c and c to a’.

(a b c) = (b c a) = (c a b)

The inverse cycle would be (c b a) = (b a c) = (a c b)

These are the only two possible cycles on three elements which move all three elements.  There are others which move fewer elements.  The complete list is (), (a b), (a c), (b c), (a b c), (a c b).  Together they form a group and we can do algebra on them if we want to.

Cycles can be combined.  Applying cycles from left to right we find (a b)(b c) = (a c b).  The order we apply the cycles matters.  (b c)(a b) = (a b c).

Clyde introduces the notation <a,b> to mean a ‘switch’ of a and b.  This is equivalent to the cycle (a b) but Clyde is keen to differentiate between the two concepts because he needs to prove that the solution can consist of distinct switches.  He combines switches in the same way as cycles.  He wraps switches in round brackets to represent the equivalent cycle.

So (<a,b>) = (a b), but the point is made that we are constructing the cycle from a switch.

Clyde also uses a ‘double-decker’ notation for cycles for clarity.  In his proof PI = (1 2 3 … k), a k-cycle.

Now whatever mix up has happened it consists of a set of k-cycles.  Clyde needs to perform another set of  k-cycles to reverse the process. Remember he cannot switch any two of the original bodies because they have already had lots of switches.  So he can only use switches that use at least one of Clyde and Ethan.

Using X to represent Clyde and Y to represent Ethan we have:

 (<x,1><x,2>…<x,i>)(<y,i+1><y,i+2>…<y,k>)(<x,i+1>)(<y,1>)

= (1 2 3 … k)(x y)

So we can reverse any cycle in this way.  At the end we can do a <x,y> switch if necessary.