Follow Up: Escaping the Beast
We can say a bit more about the Princess’s escape.
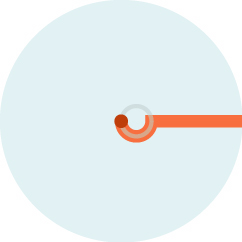
Amazingly, an optimal path for the Princess is to swim in a half circle of radius 1/8 that of the lake, then dash out to the edge.
We’ll give an analytic proof, but we could give a totally synthetic (geometric) proof as well.
An Analytic, Calculussey Proof
First of all, we should ask:
At a given moment, how fast can the Princess swim towards the edge of the lake?
Let’s not worry about our actors changing directions— this doesn’t really affect our thinking (remember we assumed they could change directions instantly). So the Beast will be dashing around the lake and the princess taking some route to get away.
Let’s scale things so that the lake has radius 1, and the Beast’s speed is 1. At time t then, he will have travelled a distance of t, and the Princess will have traveled one-fourth as far, ¼t.
At a given moment, how fast can the Princess swim towards the edge of the lake?
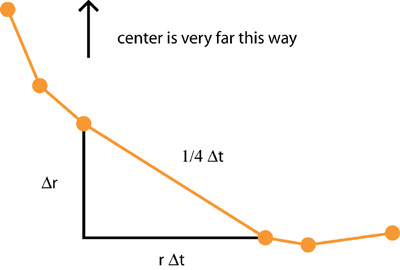
Consider what happens over a very very small interval of time, of size Δt, when the Princess is r away from the center of the lake.
The Beast travels Δt along the shore. The Princess has to keep the beast on the opposite side of the lake, and so has to swim proportionally less,
r Δt around.
How much can she increase r, if she is travelling a total of ¼ Δt, and needs only to go around a distance of r Δt? It is well worth learning how to think like an 18th Century Mathematician: essentially we have a right triangle, and can use the Pythagorean Theorem. (We don’t really have exactly a right triangle, but the difference is negligible, and as Δt decreases, is less and less important, until irrelevant in the limit.)
By the Pythagorean Theorem, an increment of change of radius Δ r is √( (¼ Δ t)2 – (r Δ t)2)
(In the limit, this is good enough; all the differences are vanishingly small compared to Δ, as Δ decreases.)
In other words, in the limit,
dr = √ (¼2–r2) dt
Using a little calculus, and remembering that at t = 0, we have r = 0 as well, we can check that
r = ¼ sin 4t
Remember that t is not only measuring time, but also the monster’s distance around the lake; the lake is radius 1, so this is also the radian measure around the lake. In other words, the initial part of the Princess’ path, in polar coordinates is:
r(θ) = ¼ sin 4θ
a circle as promised!
 mathbun.com
mathbun.com
strauss said,
December 31, 2007 at 10:04 am
Actually, this is only the optimal path of the form: curve out 1/4 of the way, then make a straight dash. Perhaps one can do better by starting to dash sooner…
stevestyle said,
January 9, 2008 at 7:56 am
I believe I can describe the solution.
The key points are:
1. The princess will never go inside the spiral/circle.
2. Wherever she ends up, she will have taken the shortest possible route.
Imagine tying one end of a piece of string to the centre of the lake (you can do that with this lake). Now hoop it around the circle and stretch it out to the edge of the lake, keeping it taught.
The path of the string is the shortest route the princess can take to reach that part of the shore.
The path is:
curve outwards for a bit;
continue in the same direction, but in a straight line, until reaching shore.
This is Chaim’s suggested path. He asks if we can improve by heading for shore earlier.
We can reach shore at the same point faster by cutting out the corner. Note that this is not the best route for the princess; it’s just a faster route for reaching the same point on shore.
We can give a range for where the optimal route lies.
If we travel a quarter circle and then head horizontally for shore then it’s easy to show this still beats the beast.
As the princess must travel at least 1, then the beast must travel at least four.
Calculating exactly where the best route lies is complex. I’ve have worked out some equations for it but not solved them. We don’t really need to know do we?
If the princess wants to land as far from the beast as possible, so she has the best safety margin, then she should swim out to _ radius then head to shore in the same direction.
The beast has to cover _ of a circle after the princess starts heading for shore, and an entire circle in total. When the princess lands the beast is still about 0.5 away.
She lands at angle theta, which has cosine _.
If we start the princess from any point on this path then this must still be the best path for her to take.
Note that this does not depend on exactly where the beast it, only on the direction from which he is coming.
Suppose we put the princess and the beast at random points, and the princess want to land as far from the beast as possible. Also assume it is best for her to head straight for shore, rather than retreat to the centre and start out from there.
She will lie on exactly one path of the type we have described, given the direction of the beast. This is her best path.
She should calculate how to land at an angle of theta while also heading away from the beast. This is her best path.
jay ha said,
March 24, 2014 at 4:55 pm
what about this variation?
An escaped prisoner finds himself in the middle of a square swimming pool. The guard that is chasing him is at one of the corners of the pool. The guard can run faster than the prisoner can swim. The prisoner can run faster than the guard can run. The guard does not swim. Which direction should the prisoner swim in in order to maximize the likelihood that he will get away?