After explaining how the Princess escaped, we pose a simple puzzle from Dennis Shasha’s new book Puzzles for Programmers and Pros.

(In the next post we’ll say a little more about the princess.)

Standard Podcast [ 8:07 ] Play Now | Play in Popup | Download

We can say a bit more about the Princess’s escape.

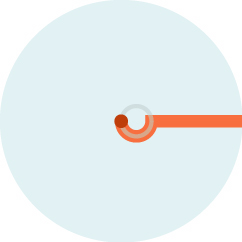
Amazingly, an optimal path for the Princess is to swim in a half circle of radius 1/8 that of the lake, then dash out to the edge.
We’ll give an analytic proof, but we could give a totally synthetic (geometric) proof as well.

Read the rest of this entry »

How can the princess escape the beast waiting on the shore?

Standard Podcast [ 2:46 ] Play Now | Play in Popup | Download

What follows after 0, 1, 2, … , once you’ve managed to list every counting number?

Around 1875, Georg Cantor created — or discovered if you like — the transfinite ordinals : the list continues 0, 1, 2, …, then ω , ω + 1, ω + 2, etc, for quite a long long way. John H. Conway tells us about his Surreal Numbers , which add in such gems as

1 / √ ω

Check out Knuth’s Surreal Numbers, Conway & Guy’s Book of Numbers , or for more advanced users, Conway’s On Numbers and Games.

Standard Podcast [ 10:04 ] Play Now | Play in Popup | Download

As B Boom wrote, the first pirate can make a proposal that gives him all but 49 (about, depending on the rules) pieces of
the gold. Read the rest of this entry »

Standard Podcast [ 10:46 ] Play Now | Play in Popup | Download

Pirates are well known for their logical and rational behavior. How should they divide up some loot?

Standard Podcast [ 11:36 ] Play Now | Play in Popup | Download

This week we consider an odd number of odd people are milling about
with water pistols, on a large flat field. At a signal, everyone turns and squirts the closest
person (We may assume, since they are just milling about randomly, there is
a unique closest person to squirt.) Show that there will always be at least
person left dry!

Standard Podcast [ 3:03 ] Play Now | Play in Popup | Download

Last week’s puzzle on Perfectly Summing Sets can be solved in many different ways; here’s one!
Read the rest of this entry »

What numbers can 1,2,4,8,16,… etc “form”? Well, every number can be “formed” by summing various powers of 2. For example, 13 = 1 + 4 + 8.

In this way, we could say that a power of 2, say 64, is “full of divisors” since it has enough divisors to form any number up to 64. Its divisors are of course 1, 2, 4, 8, 16 and 32, and we can form any number from 1 to 63 by summing up these divisors as needed.

But what other numbers of “full of divisors”?

Read the rest of this entry »

First, let’s answer last week’s puzzle on clocks!

As it turns out, there are 143 times in each twelve hour period for which you can switch the hands of a clock and still have a legitimate time! It’s easy to find these by plotting the positions of the hands throughout the day:

Read the rest of this entry »

Standard Podcast [ 7:13 ] Play Now | Play in Popup | Download

Well, we’ve been a little haphazard about posting new segments! It’s summer after all… But we’ll be back! We have quite a bit lined up for the next few months.

In the meantime, here is an interesting puzzle about ambiguous clocks. This time, for example, can be read two different ways:

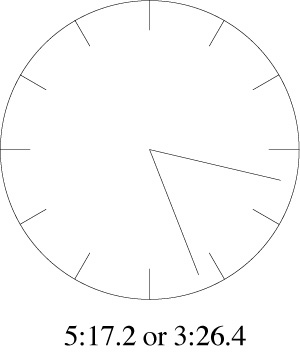
In a week or so, we’ll post the answer right here…

Standard Podcast [ 4:15 ] Play Now | Play in Popup | Download