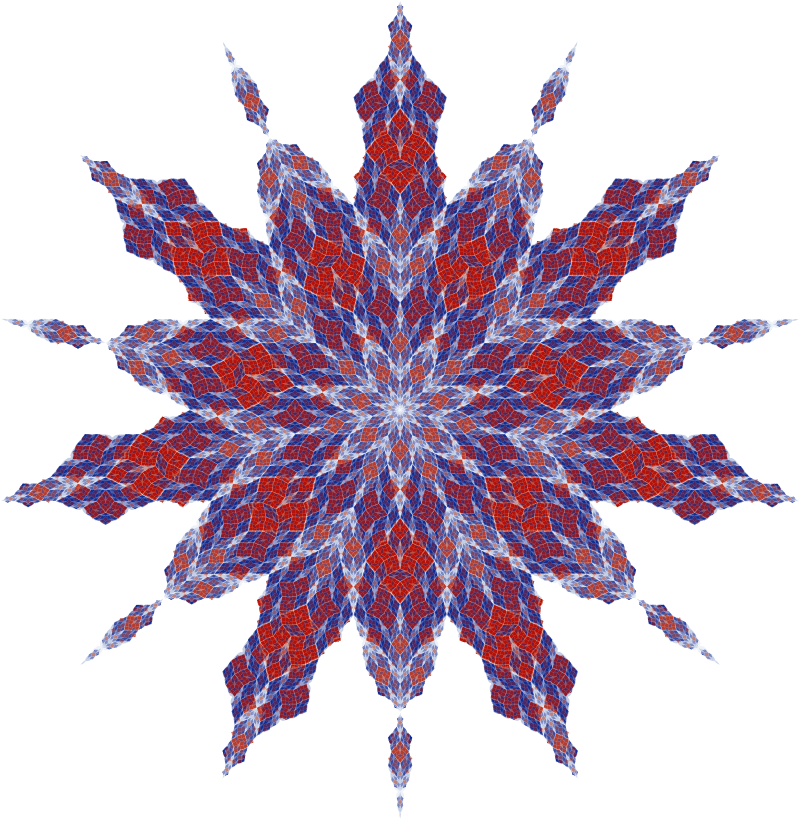
Greetings mathfactorisers!  I am one of the new wave of additional commentators on the website.  I thought I would introduce myself a little.  I am currently working as a postdoc researcher at Imperial College London, though I am also polishing my CV as my current contract finished in March.  My research is in tilings and patterns, especially those which fit onto themselves at different scales.  For those of you in London next summer I am preparing an exhibit titled “How shapes fill space” for the Royal Society Summer exhibition.  This will look at the mathematics of tilings and patterns with lots of shapes and models to play with.I also like to make pretty pictures from this research, like the example below, which is based on a tiling created by the prime mathfactor Chaim himself.   I hope to describe some of this on the mathfactor, for a taste check out my other writing at Maxwell’s demon.  This piece on rep-tiles is probably of particular interest.  For more of my pictures take a look at my website.

Standard Podcast [ 11:50 ] Play Now | Play in Popup | Download

Isaac Newton gave an elegant solution to this problem. Can you?

To understand the question, first consider the square numbers:

1 4 9 16 25 36 49 ….

Below successive squares, write the differences between them. For example, 4 – 1 = 3.

1   4   9   16   25   36   49 ....

  3   5   7    9     11    13 ....

And then repeat:

1   4   9   16   25   36   49 ....

   3   5   7    9     11    13 ....

     2   2   2     2      2  ....

It turns out that for any polynomial p, if we make a table of the values p(1), p(2), etc and take differences, successively, eventually we will have a constant row, and the number of differences we need is exactly the degree of the polynomial. For example, for 2n^3 – n, we have

 1     14      51    124    245  .....

       13   37   73   121 ....

           24   36   48  ....

               12   12 ...

(and all 12’s on this row)

Now for the puzzle!

(A warm up might be to prove the assertion above, that this works at all)

If we have just the front column of the table, we can recover the rest, and in particular, the values on the top row:

2

   1

      7 

Can only be

 
2      3    11    26    48    77 ....

     1      8     15     22  29  ....

          7       7      7     7    7  ...

It’s not too hard to figure out the polynomial that generates the values on the top row…

But more generally, give a simple formula for any polynomial in terms of the values in the first column in any such table!

(BIG WORD OF CAUTION: An elegant formula isn’t necessarily in the fully-multiplied-out form!)

Standard Podcast [ 11:14 ] Play Now | Play in Popup | Download

Pascal’s triangle, with its host of nifty tricks, provides the surprising solution to last weeks’ puzzle on sequences of averages. 

As a bonus puzzle, not mentioned in the podcast, consider the following variation with a completely different solution: Our sequence starts 

1, 1, …

Now each additional term is twice the average of all the earlier terms, not including the terms immediate predecessor! So, the third term is twice the average of 1, i.e. 2. We have now 1,1,2 …

The fourth term is twice the average of 1 & 1, i.e. 2 and we have 1,1,2,2

Continuing in this way we get 1, 1, 2, 2, 8/3, 3, etc.  The sequence wobbles around, but will grow steadily. But the remarkable thing is that the nth term, divided by n, tends to exactly (1 – 1/e^2)/2, a fact well worth trying to prove!

Our favorite new and not-so-new products of 2008!

Standard Podcast [ 17:14 ] Play Now | Play in Popup | Download

Check out these great gifts!

• Zome is an incredibly powerful construction system!
• the great puzzles of Puzzellation (available at Barnes and Nobles)
• The terrific puzzle computer game DROD
• The Magic Mirror Image Coloring Book
• The Riddles of the Sphinx by David J Bodycombe, an amazing compendium of puzzles, of hundreds of kinds, at all levels of difficulty, with historical essays to boot!
• Which leads us to Nikoli, the great Japanese puzzle co! (Rules can be found here)
• The Princeton Companion to Mathematics is a landmark classic. A must-have for every serious student, researcher or amateur.
• How Round is Your Circle just one of the many fantastic titles out on Princeton University Press
• AK Peters is another fantastic press, with a wide range of interesting math and CS titles, including, ahem, the Symmetries of Things.
• Binary Arts/ThinkFun is another source of great puzzles!
• And the authors Martin Gardner and Ivan Moscovitch are always fantastic!

Hope this helps and have fun!! Let us know how it works out!

Happy Holidays from the Math Factor!