Morris: Infinite Products
![]()
This made me smile. I hope it makes you smile too.
What is
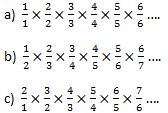
If you think they are the same then why? If you think they are different then why?
June 8, 2009 · Morris, The Mathcast · Permalink
«« Yoak: Face Up· · · FV. Singmastery! »»
![]()
This made me smile. I hope it makes you smile too.
What is
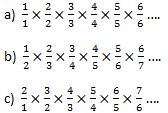
If you think they are the same then why? If you think they are different then why?
RSS feed for comments on this post · TrackBack URL
You must be logged in to post a comment.
Download a great math factor poster to print and share!
Got an idea? Want to do a guest post? Tell us about it!
Heya! Do us a favor and link here from your site!
The Math Factor Podcast is brought to you by:C Goodman-Strauss·· KUAF 91.3 FM·· Math Dept·· Univ. Ark·· XHTML ·· CSS
tjmathematica said,
June 8, 2009 at 3:54 pm
a) lim(n->infinity) PRODUCT(n/n) = 1
b) lim(n->infinity) PRODUCT(n/(n+1)) < 1
value starts at 1/2 and decreses
c) lim(n->infinity) PRODUCT((n+1)/n) > 1
value starts at 2 and increses
Brian Tristam Williams said,
June 8, 2009 at 4:38 pm
Yeah, so a) trends toward 1 :) and b) trends toward 0 and c) trends toward inifinity [and beyond!] being that c) is the reciprocal of b) but…
Hmmm… I don’t see where you get your smile from :D
Bryan said,
June 8, 2009 at 4:43 pm
The first series is obviously equal to 1 because each term is equal to 1.
For the second one, you can imagine sliding all the numbers in the denominator over one term to the right to obtain the top series, but with an extra term on the left and right of the series equal to 1/n where ‘n’ is however far you take the series. So this one is equal to zero because you can make 1/n arbitrarily small for a large enough n.
In the third one, you can imagine sliding the numerators to the right to obtain the first series but now with an extra (n/1) term left over. Making ‘n’ as big as you want means that this series taken to infinity is infinitely large.
Do I win a cake? :)
Bryan
South Africa
Brian Tristam Williams said,
June 8, 2009 at 5:12 pm
Ok, never mind, lol I get it. “Infinite Products” picture pun. tyvm
Andy said,
June 8, 2009 at 5:22 pm
The first product is very clearly 1.
If we write the second product as a partial product, then you get:
P(n) = 1/2 * 2/3 * 3/4 * … * (n-1)/n
This cancels to get P(n) = 1/n, so taking the limit gives the infinite product as 0.
The third product is the inverse of the second, so the partial product is P(n) = n. This doesn’t converge, so the infinite product diverges.
Stephen Morris said,
June 8, 2009 at 6:44 pm
Brian, thanks for getting the picture pun, it was tricky getting David Beckham and James Bond to pose for me. I’m hoping for Victoria and Moneypenny next time.
Mark said,
June 12, 2009 at 12:13 pm
a) 1
b) infinity
c) 1/infinity