GN. Benford’s Law
Benford’s Law is really quite amazing, at least at first glance: for a wide variety of kinds of data, about 30% of the numbers will begin with a 1, 17% with a 2, on down to just 5% beginning with a 9. Can you spot the fake list of populations of European countries?
| List #1 | List #2 | |
| Russia | 142,008,838 | 148,368,653 |
| Germany | 82,217,800 | 83,265,593 |
| Turkey | 71,517,100 | 72,032,581 |
| France | 60,765,983 | 61,821,960 |
| United Kingdom | 60,587,000 | 60,118,298 |
| Italy | 59,715,625 | 59,727,785 |
| Ukraine | 46,396,470 | 48,207,555 |
| Spain | 45,061,270 | 45,425,798 |
| Poland | 38,625,478 | 41,209,072 |
| Romania | 22,303,552 | 25,621,748 |
| Netherlands | 16,499,085 | 17,259,211 |
| Greece | 10,645,343 | 11,653,317 |
| Belarus | 10,335,382 | 8,926,908 |
| Belgium | 10,274,595 | 8,316,762 |
| Czech Republic | 10,256,760 | 8,118,486 |
| Portugal | 10,084,245 | 7,738,977 |
| Hungary | 10,075,034 | 7,039,372 |
| Sweden | 9,076,744 | 6,949,578 |
| Austria | 8,169,929 | 6,908,329 |
| Azerbaijan | 7,798,497 | 6,023,385 |
| Serbia | 7,780,000 | 6,000,794 |
| Bulgaria | 7,621,337 | 5,821,480 |
| Switzerland | 7,301,994 | 5,504,737 |
| Slovakia | 5,422,366 | 5,246,778 |
| Denmark | 5,368,854 | 5,242,466 |
| Finland | 5,302,545 | 5,109,544 |
| Georgia | 4,960,951 | 4,932,349 |
| Norway | 4,743,193 | 4,630,651 |
| Croatia | 4,490,751 | 4,523,622 |
| Moldova | 4,434,547 | 4,424,558 |
| Ireland | 4,234,925 | 3,370,947 |
| Bosnia and Herzegovina | 3,964,388 | 3,014,202 |
| Lithuania | 3,601,138 | 2,942,418 |
| Albania | 3,544,841 | 2,051,329 |
| Latvia | 2,366,515 | 1,891,019 |
| Macedonia | 2,054,800 | 1,774,451 |
| Slovenia | 2,048,847 | 1,065,952 |
| Kosovo | 1,453,000 | 984,193 |
| Estonia | 1,415,681 | 841,113 |
| Cyprus | 767,314 | 605,767 |
| Montenegro | 626,000 | 588,802 |
| Luxembourg | 448,569 | 469,288 |
| Malta | 397,499 | 464,183 |
| Iceland | 312,384 | 402,554 |
| Jersey (UK) | 89,775 | 94,679 |
| Isle of Man (UK) | 73,873 | 43,345 |
| Andorra | 68,403 | 41,086 |
| Guernsey (UK) | 64,587 | 34,184 |
| Faroe Islands (Denmark) | 46,011 | 32,668 |
| Liechtenstein | 32,842 | 29,905 |
| Monaco | 31,987 | 22,384 |
| San Marino | 27,730 | 9,743 |
| Gibraltar (UK) | 27,714 | 7,209 |
| Svalbard (Norway) | 2,868 | 3,105 |
| Vatican City | 900 | 656 |
Looking at these lists we have a clue as to when and how Benford’s Law works. [spoiler]
In one of the lists, the populations are distributed more or less evenly in a linear scale; that is, there are about as many populations from 1 million to 2 million, as there are from 2 million to 3 million, 3 million to 4 million etc. (Well, actually the distribution isn’t quite linear, because the fake data was made to look similar to the real data, and so has a few of its characteristics.)
The real list, like many other kinds of data, is distributed in a more exponential manner; that is, the populations grow exponentially (very slowly though) with about as many populations from 100,000 to 1,000,000; then 1,000,000 to 10,000,000; and 10,000,000 to 100,000,000. This is all pretty approximate, so you can’t take this precisely at face value, but you’ll see in the list of real data that, very roughly speaking, in any order of magnitude there are about as many populations as in any other– at least for a while.
Data like this has a kind of “scale invariance”, especially if this kind of pattern holds over many orders of magnitude. What this means is that if we scale the data up or down, throwing out the outliers, it will look about the same as before.
The key to Benford’s Law is this scale invariance. Data that has this property will automatically satisfy his rule. Why is this? If we plot such data on a linear scale it won’t be distributed uniformly but will be all stretched out, becoming sparser and sparser. But if we plot it on a logarithmic scale, (which you can think of as approximated by the number of digits in the data), then such data is smoothed out and evenly distributed.
But presto! Look at how the leading digits are distributed on such a logarithmic scale!
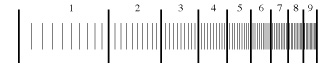
That’s mostly 1’s, a bit fewer 2’s, etc. on down to a much smaller proportion of 9’s.
[/spoiler]

 mathbun.com
mathbun.com
Rob Stevenson said,
December 19, 2009 at 6:44 am
INteresting that you suggested that data can be faked using a knowledge of Benford’s law – this is almost impossible for medium sized data sets due to the fact that anyfair sized random sampling of the data should also exhibit the law.
For example if I were a crooked accountant and wanted to reduce the tax bill for a local store I would need to amke sure that the law held for sales data sliced monthly. Or sliced by department of the store. Or by sales person. Or by payment method.
Being able to fabricate this level of distributed “semi-randomness” is *really* hard.
strauss said,
December 19, 2009 at 10:37 am
I guess the point wasn’t that we COULD fake data using Benford’s Law, but rather we should be careful not to get tripped up by some pesky investigator who is using Benford’s Law.
It’s not too hard to make up a data set from scratch that will resist any kind of slicing: just make sure your “expenses” are chosen randomly on a log scale. That is, if RAND is a random number from 0 to 1, instead of generating expenses of the form RAND*$10,000,000, generate expenses as 10^(RAND*7). No matter how the data is sliced, you’re home free! (Well, with just a few refinements depending on the particular fraud you’re perpetrating.)
You’re right, though, hiding or manipulating a specific piece of information within a larger data set is trickier. Now I’m no master criminal, but it doesn’t seem quite as bad as you say: mostly we need to carefully smear out the fraud, blending it in against the background, most especially being careful that the manipulated data is chosen with this log distribution.
(Mix a few bags of chips, DVDs, ipods, and TVs in with the rolexes, sportscars and beachfront property!)
My consulting fee can be deposited in an unmarked bank account, number available upon request.
Shawn said,
November 29, 2011 at 12:48 am
Has anyone figured out which list is fake yet?
Edwin said,
January 18, 2012 at 11:20 am
Ok, is it list two? Countries tat start with digits 4, 5, 6 and 8 appear to surpass the expected digit distribution.
Although, the 1st list also offers disparities when compared to Benford. I noted that digits 4, 6 and 7 happen a lot more than expected Benford Law. Nonetheless, he 2nd list appears more manipulated than 1st list.
Which is erroneous?
strauss said,
January 24, 2012 at 5:57 pm
Er,… unfortunately, I’ve forgotten…
Stephen Morris said,
February 1, 2012 at 6:37 pm
You can check them on line here: http://benford.cloudcontrolled.com/#
Hat tip to Ben Goldacre: http://bengoldacre.posterous.com/benfords-law-and-online-calculator-from-fun-t
Do read the article he links to.
Stephen Morris said,
February 1, 2012 at 6:44 pm
Ooh, just reading Ben Goldacre’s article again. He links to this great site which tests lots of real world data. Very nice. http://testingbenfordslaw.com/
There’s one data set which really stands out, you can probably guess before you try it. And, no, it isn’t the russian elections.