{ Hi, Steve here. Jeff asked me to post a solution and I’m more than happy to oblige. It’s a fun puzzle with some nice maths to explore. I learnt a lot about graph theory and a new theorem (new to me), Turan’s theorem. More on that later. }

In Yoak: Batteries, and the Problem-of-the Week Jeff posed a great problem from Stan Wagon’s Problem of the Week.

You have eight batteries, four good and four dead. You need two good batteries to work the device; if either battery is dead then the device shows no sign of life. How many tests using two batteries do you need to make the device work?

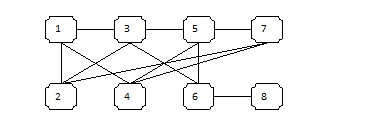
Read the rest of this entry »

Recently I discovered Stan Wagon’s Problem of the Week.  This is a delightful mailing list / site and some of the problems are in the vein of puzzles I post here.  Recent problem 1125 captured the attention of several Math Factor authors so I thought I’d post the puzzle here as an excuse to introduce you all to that list.

You have eight batteries and know that four are good and four are dead, but don’t know which are which.  Your only method of testing them is to insert two into a device that will work if you’ve put in two good batteries and not otherwise.  How many such “tests” are required in order to be sure that you’ve located two good batteries?

As of this posting, the answer to this question is not yet on the POTW website, but if you come to this later, the spoiler may be there, so be careful to avoid spoilers if you want to work this through.

Finding yourself chatting around the water cooler one afternoon, you and two co-workers agree that you would all like to know the average of your three salaries but none of you want your individual salary to be known to either of the other two.  Without need of involving any external person or machine as some sort of secret keeper, how can you achieve this end?

There are five holes in a row in my yard.  A fox lives in them moving around as follows:  Each night, it abandons it current residence and moves to an immediately neighboring hole.  If I’m allowed to check one hole each morning, identify a sequence of holes that I can check in order to be sure to catch the fox.

I recently got back in touch with an old friend and puzzler and he reminded me of a puzzle that he once told me about that confounded me for weeks.  Faced with a restatement of it, again I couldn’t come up with an answer for the life of me.  The mechanism is painfully simple, but there is something about the particulars here that short my mind out.

Combine the four number 1,3,4,and 6 with operators of addition, subtraction, multiplication and division (and parenthesis to indicate order of operation) to yield an expression equal to 24.

I assure you that you can take this in the most straight-forward manner possible.  You aren’t mean to smoosh them together to get “13″ out of 1 and 3.  You aren’t meant to use “1″ as a problem number or something of that sort.  An answer will look something like this:

(4-1)*3/6

except that is equal to 1.5 .  Your expression must equal 24.

I’m interested to hear if this is as difficult for others as it was for me.

This will be the last of my Lewis Carroll posts.  In Pillow Problems, Carroll writes:

   Three Points are taken at random on an infinite Plane.  Find the chance of their being the vertices of an obtuse-angled Triangle.

Note: An obtuse-angled triangle is one that has an angle measuring more than 90 degrees.

This puzzle is taken from a letter Carroll wrote to a 14-year-old girl named Helen Fielden.  Carroll writes:

I don’t know if you’re fond of puzzles, or not.  If you are, try this.  If not, never mind.  A gentlemen (a nobleman let us say, to make it more interesting) had a sitting-room with only one window in it — a square window, 3 feet high and 3 feet wide.  Now, he had weak eyes, and the window gave too much light, so (don’t you like “so” in a story?) he sent for the builder, and told hm to alter it, so as to give half the light.  Only, he was to keep it square — he was to keep it 3 feet high — and he was to keep it 3 feet wide.  How did he do it?  Remember, he wasn’t allowed to use curtains, or shutters, or coloured glass, or anything of that sort.

Since my last post, I actually dug up one of my books with Carroll problems.  I’ll present this one in Carroll’s own words and add a few notes:

Carroll writes:

   Some men sat in a circle, so that each had 2 neighbours; and each had a certain number of shillings.  The first had I/ more than the second, who had I/ more than the third, and so on.  The first gave I/ to the second, who gave 2/ to the third, and so on, each giving I/ more than he received, as long as possible.  There were then 2 neighbors, one of whom had 4 times as much as the other.  How many men were there?  And how much had the poorest man at first?

Notes:

A ‘/’ is clearly to be read as a shilling and the ‘I’ is to be read as 1.  With that, I think the operations is clear.  It is also clear that eventually someone will not be able to pass along 1 more shilling than he was passed, given the finite number of shillings in the game.  When that state occurs, instead of passing that person retains the shillings he was just passed.  We are then told that it is true that someone now holds 4 times as many shillings as one of his neighbors and are asked how many men there are and how many shillings the poorest of the group must have had to start.

I’ve enjoyed several books by and about Lewis Carroll with puzzles, games and neat observations.  I’m going to post a few here.  Here’s a simple one with which to get started.

Suppose that I secretly flip a coin and place either a blank or white stone in a bag based on the result.  I then put a white stone in the bag for two stones in total.  I invite you to pull one stone out and it turns out that it is white.  What is the chance that the other stone in the bag is also white?

We said during the most recent podcast that we’d offer the answer to the ending puzzle on the website.

Twitter user @snoble posted a hint on #mathfactor that points to the right answer.

First, I’ll review the problem.  You and nine other prisoners will be lined up in the morning front to back.  Each of you will have either a blue or red hat placed upon your head.  Each person can see all the hats on the heads of people in front of him, but not the color of his own or of any of the people behind.

The guards will then proceed to the rear of the line and ask that person the color of the hat on his own head.  He must guess and if he guesses wrong, sadly, he’ll be shot.  Either way, the guard then proceeds to the number nine position and repeats through all of the other prisoners.

Knowing that this will happen and with a night to plan, what strategy can the prisoners develop to maximize their expected survival rate?

Show Spoiler ▼