HQ. Newton v Leibnitz
A break from puzzling to discuss the history of the great Newton-Liebnitz dispute over the invention of Calculus, with the playwright Todd Taylor.
Archive for calculusey stuff
HJ. Strange Suitor
We’ll have some pursuit puzzles over the next couple of weeks; this segment’s puzzle has a simple and elegant solution, but it might take a while to work it out!
In the meanwhile, here’s a little discussion about the glass of water problem.
Each time we add or subtract 50%, we are multiplying the quantity of water by 1/2 or 3/2. If we began with 1 glass’ worth, at each stage, we’ll have a quantity of the form 3m/2n with m,n>0 Of course that can never equal 1, but we can get very close if m/n is very close to log3 2 = 0.63092975357145743710…
Unfortunately, there’s a serious problem: m/n has to hit the mark pretty closely in order for 3m/2n to get really close to 1, and to get within “one molecule”s worth, m and n have to be huge indeed.
How huge? Well, let’s see: an 8 oz. glass of water contains about 1025 molecules; to get within 1/1025 of 1, we need m=31150961018190238869556, n=49373105075258054570781 !! One immediate problem is that if you make a switch about 100,000 times a second, this takes about as long as the universe is old!
But there’s a more serious issue.
In a glass of water, there’s a real, specific number of molecules. Each time we add or subtract 50%, we are knocking out a factor of 2 from this number. Once we’re out of factors of 2, we can’t truly play the game any more, because we’d have to be taking fractions of water molecules. (For example, if we begin with, say, 100 molecules, after just two steps we’d be out of 2’s since 100=2*2*some other stuff.
But even though there are a huge number of water molecules in a glass of water, even if we arrange it so that there are as many 2’s as possible in that number, there just can’t be that many: 283 is about as good as we can do (of course, we won’t have precisely 8 ounces any more, but still.)
If we are only allowed 83 or so steps, the best we can do is only m= 53, n = 84 (Let’s just make the glass twice as big to accommodate that), and, as Byon noted, 3^53/2^84 is about 1.0021– not that close, really!
HH. Corpuscle Candies
In which we continue our contest for SOME interesting fact about the number 2012, describe Newton’s Law of Cooling, and ask another puzzle on the mixing liquids.
We HAVEN’T yet fully answered the coffee and cream question: a follow up post will be coming soon!
HG. Two Love
In which we confess further delight in arithmetic…
1) Send us your candidates for an interesting fact about the number 2012; the winner will receive a handsome Math Prize! As mentioned on the podcast, already its larger prime factor, 503, has a neat connection to the primes 2,3,5, and 7.
2) So what is it about the tetrahedral numbers, and choosing things? In particular, why is the Nth tetrahedral number (aka the total number of gifts on the Nth day of Christmas) is exactly the same as the number of ways of choosing 3 objects out of (N+2)? Not hard, really, to prove, but can you find a simple or intuitive explanation?
3) Finally, about those M&M’s. Maybe I exaggerated a little bit when I claimed this problem holds all the secrets of the thermodynamics of the universe, but I don’t see how! Many classic equations, such as Newton’s Law of Cooling or the Heat Equation, the laws of thermodynamics, and fancier things as well, can all be illustrated by shuffling red and blue M&M’s around. What I don’t understand is how anything got done before M&M’s were invented!
HE. On Cake and Coffee
Harry Kaplan joins us for discussion of cake and coffee– and leaves us with a counter-intuitive puzzle…
GI. Mrs Perkins’ Electric Quilt
Paul Nahin discusses his fabulous new book “Mrs Perkins Electric Quilt“, mosquitos, falling through the Earth, whether mathematics is “real” and much more!
EZ. Google, Flutes and Monopoly
We ask: What do Google, flutes and monopoly have in common? In fact, important principles behind this question apply to an astounding array of phenomena!
(Since we’ve been offline for a week or so, due to a tremendous ice storm that has paralyzed the town, we add a special bonus: the very first Math Factor episode ever aired, from January 25, 2004.)
EO. Spaghetti Loops
Just why does e appear in so many guises?
Follow Up: Escaping the Beast
We can say a bit more about the Princess’s escape.
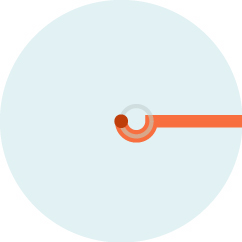
Amazingly, an optimal path for the Princess is to swim in a half circle of radius 1/8 that of the lake, then dash out to the edge.
We’ll give an analytic proof, but we could give a totally synthetic (geometric) proof as well.
BM. An astronomical cost!
The conclusion to the banana & camel puzzle.
The Math Factor in iTunes
RSS feed
Comments RSS
mathbun.com