DC. Psychology Matters
The ‘expected’ answer is not always the one people choose: Dennis Shasha explains that psychology plays a role in the answer to last week’s puzzle.
Archive for answers
DB. Envelope Mystery
Dennis Shasha answers his cake conundrum and poses a new puzzle: should you switch envelopes given the chance?
DA. A Cake Conundrum
Dennis Shasha, author of Puzzles for Programmers and Pros
joins us once again, posing a cake conundrum!
CZ. A Parlour Trick
How does this simple trick work?
Ask a friend to pick, silently, a three-digit number, then “double” it to make a six-digit number. For example, if she picks 412, the new number would be 412412. Then dividing by 7, then by 11, then by 13, presto! The original number!
Interestingly, there is no decent trick for two-digit numbers; and for four-digit numbers the trick is not so great. But for nine and fifteen digits (for the right kind of people only!!) there is a relatively simple variation.
CY. Number Sleuths
After explaining how the Princess escaped, we pose a simple puzzle from Dennis Shasha’s new book Puzzles for Programmers and Pros.
(In the next post we’ll say a little more about the princess.)
Follow Up: Escaping the Beast
We can say a bit more about the Princess’s escape.
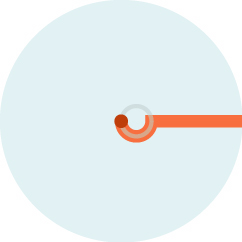
Amazingly, an optimal path for the Princess is to swim in a half circle of radius 1/8 that of the lake, then dash out to the edge.
We’ll give an analytic proof, but we could give a totally synthetic (geometric) proof as well.
CV. Dividing the Loot
As B Boom wrote, the first pirate can make a proposal that gives him all but 49 (about, depending on the rules) pieces of
the gold. Read the rest of this entry »
CU. Eminently Logical Pirates
Pirates are well known for their logical and rational behavior. How should they divide up some loot?
CT. Odd People
This week we consider an odd number of odd people are milling about
with water pistols, on a large flat field. At a signal, everyone turns and squirts the closest
person (We may assume, since they are just milling about randomly, there is
a unique closest person to squirt.) Show that there will always be at least
person left dry!
Last week’s puzzle on Perfectly Summing Sets can be solved in many different ways; here’s one!
Read the rest of this entry »
CS. Perfect Sums
First, let’s answer last week’s puzzle on clocks!
As it turns out, there are 143 times in each twelve hour period for which you can switch the hands of a clock and still have a legitimate time! It’s easy to find these by plotting the positions of the hands throughout the day:
The Math Factor in iTunes
RSS feed
Comments RSS
mathbun.com