(I have no idea why cakes are so popular in math puzzles, but here is another conundrum)
Peter Winkler gives us one more puzzle from his book Mathematical Mind Benders and tells us a little bit about why good puzzles are like good jokes.
I had a dream last night involving — (?) well I am not really sure, except that it left me wondering if there is a simple proof (if indeed it is true) that there must be a common factor of
m choose i = m!/(i! (m-i)!)
m choose j = m!/(j! (m-j)!)
for all counting numbers i,j,m with 1 < i,j < m Another way to state this same thing is: any pair of entries, on any row of Pascal's triangle (except for the 1's on the edges) will have a common factor. With facts of this sort, often there is a clever way to cast things in terms of counting something a couple of different ways which makes things clear.
Peter Winkler tell us which full house to choose, and asks: How long must we wait until all the ants fall off the rod?
Peter Winkler brings us a short poker puzzle, from his new collection Mathematical Mind Benders: What is the best full house?
(The answer is not three aces and two kings…)
The ‘expected’ answer is not always the one people choose: Dennis Shasha explains that psychology plays a role in the answer to last week’s puzzle.
Dennis Shasha answers his cake conundrum and poses a new puzzle: should you switch envelopes given the chance?
Dennis Shasha, author of Puzzles for Programmers and Pros
joins us once again, posing a cake conundrum!
How does this simple trick work?
Ask a friend to pick, silently, a three-digit number, then “double” it to make a six-digit number. For example, if she picks 412, the new number would be 412412. Then dividing by 7, then by 11, then by 13, presto! The original number!
Interestingly, there is no decent trick for two-digit numbers; and for four-digit numbers the trick is not so great. But for nine and fifteen digits (for the right kind of people only!!) there is a relatively simple variation.
After explaining how the Princess escaped, we pose a simple puzzle from Dennis Shasha’s new book Puzzles for Programmers and Pros.
(In the next post we’ll say a little more about the princess.)
We can say a bit more about the Princess’s escape.
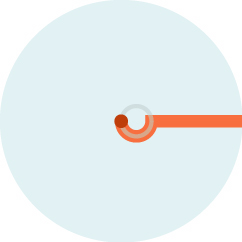
Amazingly, an optimal path for the Princess is to swim in a half circle of radius 1/8 that of the lake, then dash out to the edge.
We’ll give an analytic proof, but we could give a totally synthetic (geometric) proof as well.
Download a great math factor poster to print and share!
Got an idea? Want to do a guest post? Tell us about it!
Heya! Do us a favor and link here from your site!
The Math Factor in iTunes
RSS feed
Comments RSS
mathbun.com