CX. The Princess and A Beast
How can the princess escape the beast waiting on the shore?
Archive for math puzzles
CV. Dividing the Loot
As B Boom wrote, the first pirate can make a proposal that gives him all but 49 (about, depending on the rules) pieces of
the gold. Read the rest of this entry »
CU. Eminently Logical Pirates
Pirates are well known for their logical and rational behavior. How should they divide up some loot?
CT. Odd People
This week we consider an odd number of odd people are milling about
with water pistols, on a large flat field. At a signal, everyone turns and squirts the closest
person (We may assume, since they are just milling about randomly, there is
a unique closest person to squirt.) Show that there will always be at least
person left dry!
Last week’s puzzle on Perfectly Summing Sets can be solved in many different ways; here’s one!
Read the rest of this entry »
CS. Perfect Sums
First, let’s answer last week’s puzzle on clocks!
As it turns out, there are 143 times in each twelve hour period for which you can switch the hands of a clock and still have a legitimate time! It’s easy to find these by plotting the positions of the hands throughout the day:
CR. Clock Confusion
Well, we’ve been a little haphazard about posting new segments! It’s summer after all… But we’ll be back! We have quite a bit lined up for the next few months.
In the meantime, here is an interesting puzzle about ambiguous clocks. This time, for example, can be read two different ways:
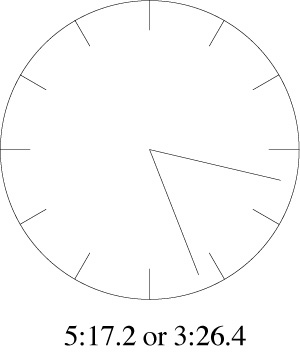
In a week or so, we’ll post the answer right here…
CP. The Prisoners Dilemma
After discussing last week’s Mismatched Pennies Game, Kyle and Chaim are hauled off to jail!
CO. Mismatched Pennies
A few months ago, we offered our listeners up to One Million Dollars! Unfortunately, we didn’t have to give away a cent, as Game Theory predicted all along.
This week, to celebrate the recent “rock scissor paper” World Championship, Kyle and Chaim play a game of “mismatched pennies”. Each puts down a penny on the table, choosing to lay the penny down showing heads or tails.
If the pennies both show heads, Chaim wins 3¢; if both show tails, Chaim wins 1¢, and if one is heads and the other tails, Kyle wins 2¢.
Thinking this through, second and triple guessing one’s opponent, is ultimately fruitless, as wonderfully illustrated in this scene from The Princess Bride
(Incidentally, game theory shows up in many movies, television shows and works of fiction!)
John von Neumann tells us, in his celebrated minimax theorem, that there is an optimal strategy for both players; each assigns a percentage to each of his options; the choice of which option to use is made randomly, by these percentages. Von Neumann tells us that there is no way to take advantage of knowing what the opponent’s optimal strategy is– that’s what makes it optimal!
But the game still might favor one player or the other, even if both are using their optimal strategy. This week’s puzzle then, is to answer: does this game of mismatched pennies favor Chaim or Kyle?
CM. Crossing the Bridge
Save Indiana, his girlfriend, his father and his father’s sidekick from certain doom! They must cross a bridge across a gorge in no more than one hour!
Read the rest of this entry »
CL. Some Number of Numbers Sum
Niclas Hedell gives his solution to the third tree puzzle he posed last week, and we ask a puzzle about sums of numbers.
The Math Factor in iTunes
RSS feed
Comments RSS
mathbun.com