How can three people, each required to guess the color of hat on their head, strategize and maximize the chances they’ll all be right?

Standard Podcast Play Now | Play in Popup | Download

Jeff Yoak discusses the mathematical – and non-mathematical – nature of poker. Sitting at the table led him to wonder: Which numbers, precisely, are the sum of consecutive integers, and in how many ways?

Standard Podcast Play Now | Play in Popup | Download

The Math Factor podcast catches up with Jeff Yoak, an author on the Math Factor website, to discuss his fantastic Find-the-Gold-Coin puzzle.

Standard Podcast Play Now | Play in Popup | Download

In working out the proof for World of Britain I came across a paradox.  Maybe smarter Math Factorites can help me out?  My sanity could depend on it.

In the puzzle you have five different tasks.  On each day one of these tasks is given at random.  How long do you expect it to take to get all five tasks?

First consider a simple case.  Suppose some event has a probability, p, of happening on any one day.  Let’s say that E(p) is the expected number of days we have to wait for the event to happen.  For example if p=1 then the event is guaranteed to happen every day and so E(p)=1.

How can we calculate E(p)? 

Read the rest of this entry »

Here’s a classic from Martin Gardner:

Suppose that you have a 3″ on a side wooden cube and a buzz saw.  You wish to cut the cube into 27 smaller cubes, each 1 cubic inch. It is easy to see that you can do this with six cuts.  You simply hold the cube in its original position while making two cuts that trisect each face.

Can it be done if fewer cuts?  If so, tell us how.  If not, prove that it can’t be done.

“It was a bright, cold day in April, and the clocks were striking thirteen.”

opens George Orwell’s novel ‘Nineteen Eighty-Four’.

1.  By an amazing coincidence thirteen squared is 169 which is the number of times my clock read the right time recently in a single calander day.  Normally it only reads correctly 164 times in a calander day.  This is even more surprising as my clock has been stopped for several years.  How can this be?

My solution combines a number of different techniques.  If you can think of any way a stopped clock can read correctly more than twice a day please post in the comments.  If you can think of something I’ve missed then we may be able to get a bigger answer!

2. I have a second clock which runs slightly fast and I have no way of adjusting it.  How can I make my clock read the right time?

3.  I noticed recently that my third clock was two minutes fast.  It runs at one minute per minute.  It tells me the right time four times a day.  Why?

For inspiration you may want to listen to Peter Sellers (Bluebottle) and Spike Milligan (Eccles) discussing the stopped-clock problem way back in 1957. 

Thanks to New Scientist’s Feedback Column and it’s readers for some of the idea’s here.

What can you say about a sequence if you know that each term is a weighted average of the terms to either side? 

For example, in the sequence 1, 2, 4, 8, 16, … each term is exactly 2/3rds of the previous term, plus 1/3rd of the following term. What other sequences have exactly that property?

For a given value p, what sequences s₁, s₂, s₃, … s_n have the property that each s_k = p s_(k-1) + (1-p) s_(k+1) ? Does knowing s₁ also fix the remaining terms? 

Amusingly, this actually will help with last weeks puzzle!

Standard Podcast [ 2:34 ] Play Now | Play in Popup | Download

A quick puzzle from one of our listeners, which has a surprising and interesting solution:

Standing at 4:00, repeatedly flip an unfair coin, moving clockwise if it comes up heads, and counterclockwise if it comes up tails.

What is the probability that you visit every hour 1-11, before you reach 12:00?

In our next post we’ll ask a seemingly unrelated question that turns out to help quite a bit…

Standard Podcast [ 1:36 ] Play Now | Play in Popup | Download

David Singmaster, Puzzler Extraordinaire, early master of the Rubik’s Cube, poser of the Singmaster Conjecture, etc, etc, engages in some wordplay.

Standard Podcast [ 11:34 ] Play Now | Play in Popup | Download

This made me smile.  I hope it makes you smile too.

What is

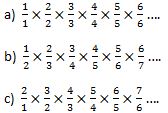
If you think they are the same then why?  If you think they are different then why?