FV. Singmastery!
David Singmaster, Puzzler Extraordinaire, early master of the Rubik’s Cube, poser of the Singmaster Conjecture, etc, etc, engages in some wordplay.
David Singmaster, Puzzler Extraordinaire, early master of the Rubik’s Cube, poser of the Singmaster Conjecture, etc, etc, engages in some wordplay.
![]()
This made me smile. I hope it makes you smile too.
What is
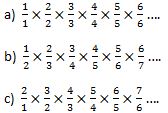
If you think they are the same then why? If you think they are different then why?
This is a classic puzzle from Martin Gardner that also appears in Peter Winkler’s Mathematical Puzzles: A Connoisseur’s Collection. (At least I think so. My copy is buried in a box somewhere.)
First, a warm-up puzzle:
You’re blindfolded and I will place two cards on the table in front of you, each either face up or face down at my option. We’ll then play a game taking turns. On your turn, you may turn over either one or both cards. On my turn, I may either swap the positions of the cards without changing which might be face up or not at my option. You are unable to detect whether or not I’ve made a swap. You win as soon as both cards are face up. Your task is to identify a set (deterministic) strategy that you can use such that regardless of how I place and switch cards you are sure to win.
[spoiler]
The strategy that you can employ to be sure to win this version is to flip both cards on your first turn, and then flip one card on your next turn. Then finally you flip both cards on your final turn.
There are three states the cards can start in: both up, both down and one of each. If they are both up, you win without taking a turn. If they are both down, your first turn causes you to win. If one is up and one is down, you maintain this state (though you reverse the cards) in your first turn. On your second turn, you either turn up the down card (and win) or turn down the up card. In this latter case, your third step of flipping both cards makes you a winner.
[/spoiler]
Now, consider a tougher version of the problem. You now have four cards, each on the corner of a square table. The setup is the same as before. You’re blindfolded and I place the cards faces up or down in a way that I think will stump you. You flip 1,2,3 or all cards on your turn, and then I either leave the table alone or rotate it 90, 180 or 270 degrees. You can’t tell if the table has turned. You then do some more flipping, etc.
(Note that I can’t arbitrarily re-order cards — only rotate the table. Their relative position remains constant. I didn’t labor this point in the first puzzle as with two cards it isn’t a distinction. You can imagine that the rules are identical and the table can only be rotated 180 degrees.)
Can you identify a pattern of steps you can take that will ensure victory regardless of my placements and turning?

I am in a total immersion game called ‘World of Britain’.
Every day you can take a daily task, if you dare. There are five tasks and each day one of these tasks is given at random. You could get the same task each day if you were unlucky.
The tasks are:
· Cycling in Edinburgh; the best city in the world has plenty of cycle lanes to help you avoid the traffic, some of them are a bit surprising.
· Cheese Rolling in Gloucestershire; can you beat the cheese?
· Bog Snorkelling in Wales; my favourite British sport, bar none! Watch the action here!
· Gurning goes back to at least the thirteenth century. You may think it is just about pulling funny faces, and you would be right.
· Mud Racing How do you know who won?
My math question is: assuming you win everything you enter how many days would you expect it to take to win all of these competitions?
p.s Gurning is now international. Here is a US gurner completely oblivious to the exciting belly-flop championship happening behind him. Apparently “everyone and their butt crack is welcome”

Thanks to my second favourite math radio programme, More or Less, for this wonderful new insight into music and maths.
In her song, Pi, Kate Bush sings the first one-hundred and fifty or so digits of the celebrity number.
This is what she sang:
3.14159265358979323846264338327950288419716939937510582319749
44592307816406286208 8214808651328230664709384460955058223
You don’t need me to point out the wrong digits do you? Good. Then we can move on.
This has led to the Kate Bush Conjecture. Since Pi contains an infinite sequence of digits which never repeat surely the sequence Kate sings must occur somewhere! She never says she is starting at the beginning.
The Weak Kate Bush Conjecture says:
The sequence Kate sings exists somewhere in the decimal expansion of Pi.
The Strong Kate Bush Conjecture says:
Kate could have sung any finite sequence of digits and it would exist somewhere in the decimal expansion of Pi.
If Pi were a random sequence of digits then both conjectures are true. But Pi isn’t random, it is a well-defined number so we can’t make any assumptions. Instinctively I think it must be true, but that isn’t good mathematics, we need to prove it!
For example the following number is infinite and non-repeating but it doesn’t satisfy either conjecture: 0.01001100011100001111…
If the strong conjecture is true then every finite sequence exists in Pi. And they each exist an inifinite number of times since they can occur in an infinite number of longer sequences. Think about that, an infinite number of sequences each occurs an infinite number of times.
Everything that can be encoded digitally would occur within Pi. That would include the complete works of Shakespeare, naturally, and also the note you left for the milkman last Tuesday, and those poems you wrote when you were five.
Every religious book, all cannons and all translations, both forwards and backwards. Every prayer, every satanic chant and every children’s song.
That picture of the cosmic microwave background, the observations of Tycho Brahe and all of Kepler’s notes; and the results from CERN that will prove the Higgs-Boson (come on guys!)
It would include everything on your iPod, every episode of Math Factor and an alternative Math Factor with Groucho Marx.
Every album by Bob Dylan, or Kate Bush. And everything you’ve sung in the shower.
It would include this post and all the comments you will make, or think about making.
It would include every thought and idea you have ever had, or ever will have, or ever could have. (Gödel may have something to say about that)
And you thought Kate Bush was just a singer.
And you thought Pi was just a number.
Arp and Bif are at a party; every guest shakes hands a different number of times — except Arp and Bif, who shake hands the same number times as one another.
How many times did Arp and Bif shake hands?
(Well, that’s not quite enough information, all you need to know is the exact number of guests — and it turns out that there are only two possibilities in any case.)
We also answer last weeks puzzle and ‘fess up about the cards in the dark problem.
Rob Fathauer discusses the ins and outs of the mathematical toy business, and we ask: For which numbers is the sum of digits the same as the sum of digits of twice the number. For example:
The sum of the digits of 351 is 9 and the sum of the digits of 2 x 351 = 702 is also 9.
1) If a number has this property, can we always rearrange its digits and obtain another number with this property (513, 135, etc all have it)
2) Which powers of 2 have this property?
3) And most of all, can you give a simple characterization of the numbers with this property, in terms of just the digits themselves?
I have in front of me three boxes. One contains all red balls. One contains all blue balls. The third contains a mixture of red and blue balls. The three boxes are labeled as to their contents, and the three labels correspond to possible contents of a box, but you know that the labels are all misplaced.
You may draw one ball (at random) out of a box of your chosing. After that, you must rearrange the labels so that they correctly reflect the contents of the boxes. How do you do this?
Dr. Karl Schaffer, of MathDance shows us (as best you can on an audio podcast!) two body movements involving interesting higher level mathematics:
The Portuguese Waiter Trick: You can rotate your hand, palm upwards, a full 720°, returning to your starting position!
This reflects an amazing mathematical fact: that if you perform any full rotation twice you reach a configuration that can be morphed steadily back to the original state, without any rotations at all! In the waiter trick, this morphing back to the original state is cleverly being carried out even as the rotations are being undertaken.
(There is a very beautiful way to understand this, which is a little outside the scope of our podcast; but essentially, the rotations of the sphere themselves form a special topological space; within that space, a loop is a series of rotations that takes you back to your starting point. The essential fact is that every “doubled loop”— every loop made by going around another loop twice— is contractible, can be shrunk to a point. In other words, if we perform two full rotations, we can morph our chain of rotations back to having done nothing.
As another illustration, hold one end of a belt fixed and rotate the other end 720°. The twists all along the belt are like a chain of rotations (a path through our space of rotations). Can you find a way to remove the twist without rotating either end? This is sometimes called the Dirac Belt Trick, after the famous physicist, Paul Dirac.
This is a quickie that came out of my computer programming work adapted as a puzzle.
I propose to stand in front of you with a bag of balls. I will hand you the balls one at a time. You have no idea how many balls my bag contains. I will also provide you with a magic device such that when its button is pushed, it provides you with a random number between 0 and 1. You may use this as often as you like.
You must hold on to exactly one ball at a time. When I hand you a ball, you must either throw it away immediately or else retain it and throw away the ball that you were previously holding. After you have either retained or thrown away the last ball, your goal is for there to be an exactly equal chance that you are currently holding each of the balls that I have handed you.
It may help to provide a similar problem to demonstrate how you might use the magical device to accomplish something similar. Suppose that I told you in advance that there were ten balls. You could then use the device to generate your random number and multiply that number by 10. This would give you a random number between 0 and 10 uniformly distributed over that range. You could then designate all numbers up to 1 as pointing to the first ball, numbers greater than 1 up to 2 as the second ball, etc. Your strategy would then be to throw away balls until handed the ball corresponding to your number and retaining that one from then on. With this strategy, you would retain each of the balls with an exactly 10% chance.
This method can’t be directly adapted to the puzzle because you wouldn’t know what multiple to use before the first draw because you don’t know how many balls will be present, so you’ll need another strategy.