Prof. Bernie Madison discusses his innovative course at the University of Arkansas; thinking straight about mathematics is fundamental for an informed and capable citizenry– but why doesn’t mathematics education seem to foster this?
The ‘expected’ answer is not always the one people choose: Dennis Shasha explains that psychology plays a role in the answer to last week’s puzzle.
Dennis Shasha answers his cake conundrum and poses a new puzzle: should you switch envelopes given the chance?
Dennis Shasha, author of Puzzles for Programmers and Pros
joins us once again, posing a cake conundrum!
How does this simple trick work?
Ask a friend to pick, silently, a three-digit number, then “double” it to make a six-digit number. For example, if she picks 412, the new number would be 412412. Then dividing by 7, then by 11, then by 13, presto! The original number!
Interestingly, there is no decent trick for two-digit numbers; and for four-digit numbers the trick is not so great. But for nine and fifteen digits (for the right kind of people only!!) there is a relatively simple variation.
After explaining how the Princess escaped, we pose a simple puzzle from Dennis Shasha’s new book Puzzles for Programmers and Pros.
(In the next post we’ll say a little more about the princess.)
We can say a bit more about the Princess’s escape.
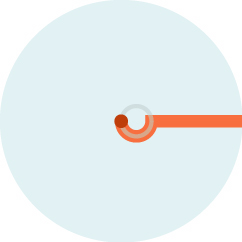
Amazingly, an optimal path for the Princess is to swim in a half circle of radius 1/8 that of the lake, then dash out to the edge.
We’ll give an analytic proof, but we could give a totally synthetic (geometric) proof as well.
How can the princess escape the beast waiting on the shore?
What follows after 0, 1, 2, … , once you’ve managed to list every counting number?
Around 1875, Georg Cantor created — or discovered if you like — the transfinite ordinals : the list continues 0, 1, 2, …, then ω , ω + 1, ω + 2, etc, for quite a long long way. John H. Conway tells us about his Surreal Numbers , which add in such gems as
1 / √ ω
Check out Knuth’s Surreal Numbers, Conway & Guy’s Book of Numbers , or for more advanced users, Conway’s On Numbers and Games.
As B Boom wrote, the first pirate can make a proposal that gives him all but 49 (about, depending on the rules) pieces of
the gold. Read the rest of this entry »
Download a great math factor poster to print and share!
Got an idea? Want to do a guest post? Tell us about it!
Heya! Do us a favor and link here from your site!
The Math Factor in iTunes
RSS feed
Comments RSS
mathbun.com