Pirates are well known for their logical and rational behavior. How should they divide up some loot?

Standard Podcast [ 11:36 ] Play Now | Play in Popup | Download

This week we consider an odd number of odd people are milling about
with water pistols, on a large flat field. At a signal, everyone turns and squirts the closest
person (We may assume, since they are just milling about randomly, there is
a unique closest person to squirt.) Show that there will always be at least
person left dry!

Standard Podcast [ 3:03 ] Play Now | Play in Popup | Download

Last week’s puzzle on Perfectly Summing Sets can be solved in many different ways; here’s one!
Read the rest of this entry »

What numbers can 1,2,4,8,16,… etc “form”? Well, every number can be “formed” by summing various powers of 2. For example, 13 = 1 + 4 + 8.

In this way, we could say that a power of 2, say 64, is “full of divisors” since it has enough divisors to form any number up to 64. Its divisors are of course 1, 2, 4, 8, 16 and 32, and we can form any number from 1 to 63 by summing up these divisors as needed.

But what other numbers of “full of divisors”?

Read the rest of this entry »

First, let’s answer last week’s puzzle on clocks!

As it turns out, there are 143 times in each twelve hour period for which you can switch the hands of a clock and still have a legitimate time! It’s easy to find these by plotting the positions of the hands throughout the day:

Read the rest of this entry »

Standard Podcast [ 7:13 ] Play Now | Play in Popup | Download

Well, we’ve been a little haphazard about posting new segments! It’s summer after all… But we’ll be back! We have quite a bit lined up for the next few months.

In the meantime, here is an interesting puzzle about ambiguous clocks. This time, for example, can be read two different ways:

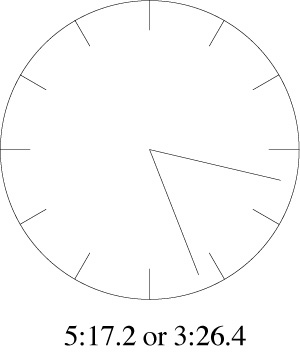
In a week or so, we’ll post the answer right here…

Standard Podcast [ 4:15 ] Play Now | Play in Popup | Download

Bill Poundstone, author of The Prisoner’s Dilemma, tells us some game theory lore, how to model an arms race, and lessons for the good life.

Standard Podcast [ 15:59 ] Play Now | Play in Popup | Download

After discussing last week’s Mismatched Pennies Game, Kyle and Chaim are hauled off to jail!

Read the rest of this entry »

Standard Podcast [ 14:32 ] Play Now | Play in Popup | Download

A correspondent writes:

Greetings,

I think that in the long run both strategies are equivalent. This game doesn’t favor any player.

Demonstration

Chaim Expected Gains = 3 * 1/4 + 1 * 1/4 = 1

Kyle Expected Gains = 1/4 * 2 + 1/4 * 2 = 1

This is so if both of us pick H half of the time, and pick T half of the time.

But!

If I know Kyle is going to pick H half of the time and T half of the time, I should adjust my strategy. I can do better by always picking H; the payout would then be

C: 3*1/2 = 3/2
K: 2*1/2 = 1
Net 1/2 in my favor!!

Conversely, if I am picking H half of the time and T half of the time, Kyle should adjust his strategy and choose T all of the time; this comes out to

C: 1*1/2 = 1/2
K: 2*1/2 = 1
Net 1/2 in Kyle’s favor– rats!

John von Neumann’s celebrated result is that both players have an optimal strategy, one that cannot be exploited by the other player. If we both play optimally, is the game balanced?

Steve D. wrote us to say:

I was listening to another podcast and they misread the copy and ended up
saying “What is the most numerous number?”. Well, what IS the most numerous number?

This is really a fascinating question! Have you ever wondered, for example, why there are 7 of so many things:

• 7 wonders of the ancient world
• 7 mortal sins
• 7 stars in the big dipper
• 7 days of the week
• 7 dwarves
• 7 brides for 7 brothers
• 7 items on this list

Really, it’s not that big of a mystery. The fact is, small numbers are very useful, and get called upon a lot. But there aren’t that many of them to go around.

Hence, the First Strong Law of Small Numbers: There aren’t enough small numbers to meet the many demands placed upon them!

The most numerous numbers, in a sense then, are the small ones. Google searches seem to confirm this:

• 1, 2, 3, 4, … (several billion hits each)
• 78, 122, 157, … (several hundreds of millions of hits each)
• 12122…(millions of hits)
• 1278232… (hundreds of hits)

Lotsa fun can be had in this way… With a little fishing, you can find some ridiculously large numbers with more hits than they deserve, but the principle is clear.

This same principle, incidentally, explains why, for example, the Golden Ratio appears in so many settings. There’s nothing really that mystical about it. The Golden Ratio is a root of the polynomial x²-x-1=0. Roots of polynomials come up all over the place, in countless applications. And just as small numbers are in great demand, roots of simple polynomials will appear over and over again.

The Golden Ratio is just about the simplest non-integer root possible, and so, of course, shows up endlessly.

Challenge Question I’m kind of curious now: What is the smallest counting number that is NOT on the web?

210210876 was not on the web until just now, according to Google. Internet history has just been made!! But I’m sure you can find something smaller…

A few months ago, we offered our listeners up to One Million Dollars! Unfortunately, we didn’t have to give away a cent, as Game Theory predicted all along.

This week, to celebrate the recent “rock scissor paper” World Championship, Kyle and Chaim play a game of “mismatched pennies”. Each puts down a penny on the table, choosing to lay the penny down showing heads or tails.

If the pennies both show heads, Chaim wins 3¢; if both show tails, Chaim wins 1¢, and if one is heads and the other tails, Kyle wins 2¢.

Thinking this through, second and triple guessing one’s opponent, is ultimately fruitless, as wonderfully illustrated in this scene from The Princess Bride
(Incidentally, game theory shows up in many movies, television shows and works of fiction!)

John von Neumann tells us, in his celebrated minimax theorem, that there is an optimal strategy for both players; each assigns a percentage to each of his options; the choice of which option to use is made randomly, by these percentages. Von Neumann tells us that there is no way to take advantage of knowing what the opponent’s optimal strategy is– that’s what makes it optimal!

But the game still might favor one player or the other, even if both are using their optimal strategy. This week’s puzzle then, is to answer: does this game of mismatched pennies favor Chaim or Kyle?

Standard Podcast [ 16:26 ] Play Now | Play in Popup | Download