Morris: Follow Up: Triel/Truel/Whatever
This is the solution to Morris: Trial/Trual/Whatever. Please look there before reading the solution.
It turns out the right word is truel, first coined in 1954 by Martin Shubik.
This is the solution to Morris: Trial/Trual/Whatever. Please look there before reading the solution.
It turns out the right word is truel, first coined in 1954 by Martin Shubik.
I’m overdue to post a puzzle, but I’m momentarily tapped out. Here’s a curiosity in the meantime: You can provide a very good estimate of a conversion from miles to kilometers by choosing sequential Fibonacci numbers. The conversion rate is 1.609344 kilometers to a mile. So this gives us:
| 1 | 2 | 1.609 |
| 2 | 3 | 3.219 |
| 3 | 5 | 4.828 |
| 5 | 8 | 8.047 |
| 8 | 13 | 12.875 |
| 13 | 21 | 20.921 |
| 21 | 34 | 33.796 |
| 34 | 55 | 54.718 |
| 55 | 89 | 88.514 |
| 89 | 144 | 143.232 |
| 144 | 233 | 231.746 |
| 233 | 377 | 374.977 |
| 377 | 610 | 606.723 |
| 610 | 987 | 981.700 |
| 987 | 1597 | 1588.423 |
This leaves you in pretty good shape if you need to get from Cincinnati, OH to Destin, FL at 610 Miles, but what if you need to convert some distance that doesn’t happen to be a Fibonacci number? Just build it up from parts!
100 miles is 89+8+3. So in kilometers, that’s 144 + 13 + 5 or 162 kilometers. (160.9344 by conversion…)
OK. Here’s a puzzle, sort of. I found this interesting set of numbers recently:
{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 53, 371, 5141, 99481 }
The series doesn’t continue. That’s all of them. What’s special about those numbers?
Mrs Smith has two children. The eldest is a boy. What is the chance that both are boys?
Mrs Jones has two children. One is a boy. What is the chance that both are boys?
Mrs Brown has two children. One is a boy born on a Tuesday. What is the chance that both are boys?
From Gary Foshee published on Ed Pegg’s http://www.mathpuzzle.com/

When two men get up ridiculously early to fire pistols at each other we call it a duel. Personally I prefer to lie in.
But what is the right term when three men skip breakfast to fire pistols at each other?
In a cold, misty field near the outskirts of Paris the sun peers over the horizon to see three men face each other with pistols. Xavier is an expert shot, he never misses. Jean-Christophe is a very good shot, he will get you four times out of five. Francois only has a fifty/fifity chance of hitting his target.
They each take turns to fire their pistol.
What is the best strategy for each of them and what odds would you give for the last man standing?
After the bodies had been cleared away I started to wander home only to hear the referee say ‘Maintenant, M. Galois et ami’
No, we are not kidding about the gravity of the extraneous zero problem. We must speak out now, before the end of the decade and attention fades.
In Living With Crazy Buttocks, Stephen Morris told us of a rather interesting party. The story continues…
After winning their trip to Paris, the guests became elated and celebrated with the consumption of some adult beverages. Ever responsible, the host confiscated the keys to all cars to ensure that no one drove home drunk. Later on, when things started to calm down, party-goers started to request the return of their keys claiming to be sober enough for the drive home.
Having once been out-done by the guests, our host took another whack. He distributed all of the keys, but did so randomly. He then presented a challenge he felt sure they’d only be able to satisfy if they were indeed sober enough to drive. They were allowed to exchange keys, but only in rounds. During each round, each party-goer could either do nothing or pair up with another party-goer and exchange the sets of keys each was holding. (Each party-goer could be part of at most one pairing per round.) No one would be allowed to drive home unless everyone recovered their own keys.
The host wished to allow only a fixed number of rounds. To be fair, he wanted to be sure that it would indeed be possible to make the change. However, he also wanted to make it as difficult as possible for the party-goers. What is the minimum number of rounds must allow them to ensure that an exchange would be possible?
For clarity, all key recipients can discuss, share information such as who has the keys of whom, and agree upon a strategy. Also, careful readers will realize that there were 20 guests at the party originally. Sadly, it was a rather disorderly party and some guests did leave early, but many more appeared. Everyone present at the key ceremony had a key confiscated, and everyone with a key confiscated received a key for this challenge, but neither you nor the host knows just how many there are.
{ Hi, Steve here. Jeff asked me to post a solution and I’m more than happy to oblige. It’s a fun puzzle with some nice maths to explore. I learnt a lot about graph theory and a new theorem (new to me), Turan’s theorem. More on that later. }
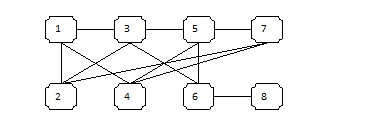
In Yoak: Batteries, and the Problem-of-the Week Jeff posed a great problem from Stan Wagon’s Problem of the Week.
You have eight batteries, four good and four dead. You need two good batteries to work the device; if either battery is dead then the device shows no sign of life. How many tests using two batteries do you need to make the device work?
Here’s an idea for a general tiling game. Start with a set of shapes and 2 (or more) people. Each person takes it in turn to place onto a patch of tiling. The winner is the last person to move.
So here’s the puzzle:
Take the Myer’s polyhex tile:

Can you:
I personally have no idea, so this is a challenge problem!
If you have access to a Laser Cutter or other fancy computer device the cut files are on Thingiverse.
So, I’m teaching a new course, Math 2033, Mathematical Thought, and it’s going great! I’d like to take a moment to write about it!
(This is one reason the MF has been kinda slow lately; another is that I’m chair) When it’s fully up and running, we’ll have about 150 students in one large section each semester (we’re starting with about 100). In a nutshell, it’s the Math Factor, as a course.
Michael Huber discusses the mathematics of the Twelve Labors of Hercules!